题目内容
设f（x），g（x）分别是定义在R上的奇函数和偶函数，当f′（x）g（x）-f（x）g′（x）＜0对任意x∈[0，+∞）恒成立，则不等式
＜0的解集是（ ）
| f(x) |
| g(x) |
| A、（-∞，0] |
| B、[0，+∞） |
| C、（-∞，0） |
| D、（0，+∞） |
考点：利用导数研究函数的单调性,函数的单调性及单调区间
专题：导数的综合应用
分析：求函数式
的导数，判断函数的单调性，根据函数的单调性即可解不等式．
| f(x) |
| g(x) |
解答：
解：∵f′（x）g（x）-f（x）g′（x）＜0对任意x∈[0，+∞）恒成立，
∴[
]′=
＜0，即当x≥0时，函数
单调递减，
∵f（x），g（x）分别是定义在R上的奇函数和偶函数，
∴
是奇函数，且
=0，
则定义域R上函数
单调递减，
则不等式
＜0的解集是（0，+∞），
故选：D
∴[
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
| f(x) |
| g(x) |
∵f（x），g（x）分别是定义在R上的奇函数和偶函数，
∴
| f(x) |
| g(x) |
| f(0) |
| g(0) |
则定义域R上函数
| f(x) |
| g(x) |
则不等式
| f(x) |
| g(x) |
故选：D
点评：本题主要考查不等式的解法，构造函数利用函数单调性和导数之间的关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图的程序输出的结果是（ ）
| A、3 | B、5 | C、9 | D、13 |
函数f（x）=x2-2lnx的增区间为（ ）
| A、（1，+∞） | ||
| B、（0，1） | ||
C、（
| ||
D、（0，
|
关于x的不等式x2-ax+a＞0（a∈R）在R上恒成立的充分不必要条件是（ ）
| A、a＜0或a＞4 |
| B、0＜a＜2 |
| C、0＜a＜4 |
| D、0＜a＜8 |
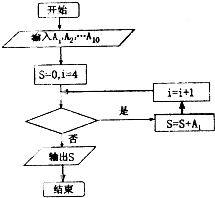如表是我市抽查部分高中学生的身高统计表，从左到右的各组表示的学生人数依次记为A1，A2，…，A10（如A2表示身高[150，155）内的人数），如图是统计表中身高在一定范围内的学生人数的程序框图，如果要统计身高在160-180cm（含160cm不含180cm）的学生人数，那么空白的判断框内应填写的条件是（ ）