题目内容
已知球的一个内接正三棱锥的三视图如下所示，则该球的表面积是 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中球的一个内接正三棱锥的三视图，可求出球的半径，进而求出球的表面积．
解答：
解：由已知中正三棱锥的三视图，
可得该三棱锥是由一个棱长为
的正方体截去四个角得到的，
其外接球即为棱长为
的正方体的外接球，
故其外接球半径为：
，
故该球的表面积S=4πR2=6π，
故答案为：6π
可得该三棱锥是由一个棱长为
| 2 |
其外接球即为棱长为
| 2 |
故其外接球半径为：
| ||
| 2 |
故该球的表面积S=4πR2=6π，
故答案为：6π
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
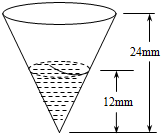“降水量”是指从天空降落到地面上的液态或固态（经融化后）降水，未经蒸发、渗透、流失而在水平面上积聚的深度．降水量以mm为单位．为了测量一次降雨的降水量，一个同学使用了如图所示的简易装置：倒置的圆锥．雨后，用倒置的圆锥接到的雨水的数据如图所示，则这一场雨的降水量为一几何体的正视图和侧视图是边长为2的等边三角形，俯视图是直径为2的圆，则此几何体的表面积为（ ）
A、4π+2
| ||
B、2π+2
| ||
| C、3π | ||
| D、2π |