题目内容
双曲函数是一类在物理学上是有十分广泛应用的函数,并且它具有与三角函数相似的一些性质,下面给出双曲函数的定义:双曲正弦函数shx=
,双曲余弦函数:chx=
,则函数y=ch(2x)-chx+(shx)2-(chx)2的值域是 .
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
考点:函数的值域
专题:函数的性质及应用
分析:由新定义把函数y=ch(2x)-chx+(shx)2-(chx)2化简,然后令t=ex+e-x换元,再利用二次函数的单调性求得函数值域.
解答:
解:由shx=
,chx=
,得
y=ch(2x)-chx+(shx)2-(chx)2=
-
+(
)2-(
)2
=
-
+
=
-1
=
-2
=
(t2-t-4)(t=ex+e-x≥2),
∵y=
(t2-t-4)在[2,+∞)上为增函数,
∴其值域为[-1,+∞).
∴函数y=ch(2x)-chx+(shx)2-(chx)2的值域是[-1,+∞).
故答案为:[-1,+∞).
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
y=ch(2x)-chx+(shx)2-(chx)2=
| e2x+e-2x |
| 2 |
| ex+e-x |
| 2 |
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
=
| e2x+e-2x |
| 2 |
| ex+e-x |
| 2 |
| e2x+e-2x-2-e2x-e-2x-2 |
| 4 |
=
| e2x+e-2x-(ex+e-x) |
| 2 |
=
| (ex+e-x)2-(ex+e-x) |
| 2 |
=
| 1 |
| 2 |
∵y=
| 1 |
| 2 |
∴其值域为[-1,+∞).
∴函数y=ch(2x)-chx+(shx)2-(chx)2的值域是[-1,+∞).
故答案为:[-1,+∞).
点评:本题是新概念题,考查了函数值域的求法,考查了换元法,训练了利用函数单调性求函数值域,是中档题.

练习册系列答案
相关题目
同时抛掷两枚质地均匀的相同的骰子,记“出现点数为4,5“的事件为P1,“出现点数为6,6“的事件为P2,则下列结论正确的是( )
| A、P1=P2 |
| B、P1>P2 |
| C、P1<P2 |
| D、P1、P2大小无法确定 |
若一个圆柱的侧面展开图是一个边长为2π的正方形,则这个圆柱的表面积是( )
| A、4π2 |
| B、2π+4π2 |
| C、8π2 |
| D、4π+8π2 |
命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是( )
| A、使用了归纳推理 |
| B、使用了类比推理 |
| C、使用了“三段论”,但推理形式错误 |
| D、使用了“三段论”,但小前提错误 |
若直线y=a与函数y=sinx的图象相交,则相邻的两交点间的距离的最大值为( )
A、
| ||
| B、π | ||
C、
| ||
| D、2π |

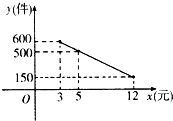 某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.
某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.