题目内容
15.已知f(x)=(x2-3)ex(其中x∈R,e是自然对数的底数),当t1>0时,关于x的方程[f(x)-t1][f(x)-t2]=0恰好有5个实数根,则实数t2的取值范围是( )| A. | (-2e,0) | B. | (-2e,0] | C. | [-2e,6e-3] | D. | (-2e,6e-3) |
分析 求出f(x)的导数,单调区间和极值,画出f(x)的大致图象,讨论t1的范围,确定t2的范围,通过图象即可得到所求范围.
解答 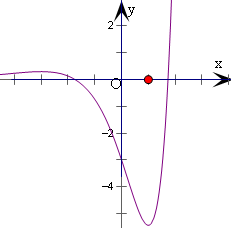 解:f(x)=(x2-3)ex的导数为
解:f(x)=(x2-3)ex的导数为
f′(x)=(x2+2x-3)ex=(x-1)(x+3)ex,
当-3<x<1时,f′(x)<0,f(x)递减;
当x>1或x<-3时,f′(x)>0,f(x)递增.
可得f(x)的极小值为f(1)=-2e,极大值为f(-3)=6e-3,
作出y=f(x)的图象,如图:
当t1>0时,关于x的方程[f(x)-t1][f(x)-t2]=0
恰好有5个实数根,
即为f(x)=t1或f(x)=t2恰好有5个实数根,
若t1>6e-3,f(x)=t1只有一个实根,不合题意;
若0<t1<6e-3,f(x)=t1有三个实根,只要-2e<t2≤0,满足题意;
若t1=6e-3,f(x)=t1有两个实根,只要0<t2<6e-3,满足题意;
综上可得,t2的范围是(-2e,6e-3).
故选:D.
点评 本题考查函数和方程的转化思想,考查数形结合思想方法运用,以及导数的运用:求单调区间和极值,属于中档题.

练习册系列答案
相关题目
5.一次函数y=-$\frac{m}{n}$x+$\frac{1}{n}$的图象同时经过第一、二、四象限的必要不充分条件是( )
| A. | mn>0 | B. | m>1,且n>1 | C. | m>0,且n<0 | D. | m>0,且n>0 |
6.已知sin(π+α)=$\frac{1}{2}$,则cos(α-$\frac{3}{2}$π)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
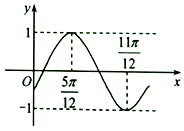 函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(0)=$-\frac{{\sqrt{3}}}{2}$.
函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(0)=$-\frac{{\sqrt{3}}}{2}$.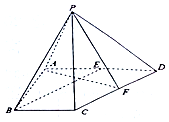 如图,在四棱锥P-ABCD中,△PCD为等边三角形,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=2BC=2,AB=$\sqrt{3}$,点E、F分别为AD、CD的中点.
如图,在四棱锥P-ABCD中,△PCD为等边三角形,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=2BC=2,AB=$\sqrt{3}$,点E、F分别为AD、CD的中点.