题目内容
11.已知函数$f(x)=\left\{\begin{array}{l}x+4,-3≤x≤0\\{x^2}-2x,0<x<4\\-x+2,4≤x≤5\end{array}\right.$,则f[f(f(2))]=( )| A. | 2 | B. | -2 | C. | 4 | D. | 0 |
分析 利用分段函数由里及外逐步求解即可.
解答 解:函数$f(x)=\left\{\begin{array}{l}x+4,-3≤x≤0\\{x^2}-2x,0<x<4\\-x+2,4≤x≤5\end{array}\right.$,
则f[f(f(2))]=f[f(4-4)]=f[f(0)]=f(0+4)=f(4)=-4+2=-2..
故选:B.
点评 本题考查分段函数的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
20.设双曲线的中心在原点,焦点在x轴上,离心率e为$\sqrt{5}$,则该双曲线的两条渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{1}{2}x$ | C. | y=±4x | D. | y=±x |
1.若抛物线C1:y=$\frac{1}{4}$x2的焦点F到双曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的距离为$\frac{\sqrt{3}}{2}$,抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=-1的距离之和的最小时为$\sqrt{5}$,则双曲线C2的方程为( )
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
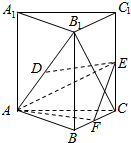 已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.
已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.
 如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.
如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.