题目内容
已知数列{an}的通项公式an=
,求数列{an}中的最大值.
| n |
| n2+90 |
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:an=
=
.由y=n+
,可得函数在(1,9)上单调递减,在(9,+∞)上单调递增,可得n=9时,n+
取得最小值19,即可求数列{an}中的最大值.
| n |
| n2+90 |
| 1 | ||
n+
|
| 90 |
| n |
| 90 |
| n |
解答:
解:an=
=
.
由y=n+
,可得函数在(1,9)上单调递减,在(9,+∞)上单调递增,
∴n=9或10时,n+
取得最小值19,
∴数列{an}中的最大值为
.
| n |
| n2+90 |
| 1 | ||
n+
|
由y=n+
| 90 |
| n |
∴n=9或10时,n+
| 90 |
| n |
∴数列{an}中的最大值为
| 1 |
| 19 |
点评:本题考查数列递推式,考查函数的单调性,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在R上的函数f(x)的图象关于点(a,b),(c,b)都对称(a≠c),则( )
| A、f(x)是以|a-c|为周期的函数 | ||
| B、f(x)是以2|a-c|为周期的函数 | ||
C、f(x)是以
| ||
| D、f(x)不是周期函数 |
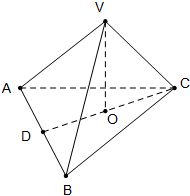 如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB=
如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB= 如图所示的圆中,已知圆心角∠AOB=
如图所示的圆中,已知圆心角∠AOB=