题目内容
1．已知函数g（x）=f（x）-x是偶函数，且f（3）=4，则f（-3）=（ ）| A． | -4 | B． | -2 | C． | 0 | D． | 4 |
分析 利用函数的奇偶性，真假求解函数值即可．
解答 解：函数g（x）=f（x）-x是偶函数，
可知g（3）=g（-3），
可得f（3）-3=f（-3）+3，
即4-3=f（-3）+3，
f（-3）=-2．
故选：B．
点评 本题考查函数的奇偶性的应用，考查计算能力．
练习册系列答案
相关题目
12．△ABC的三内角A，B，C所对边长分别是a，b，c，若$\frac{sinB-sinA}{sinC}$=$\frac{{\sqrt{3}a+c}}{a+b}$，则角B的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{5π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
9．已知复数z=1+i，则$\frac{{|{z-1}|}}{\overline{z}-1}$的值等于（ ）
| A． | i | B． | -i | C． | 1 | D． | -1 |
16．已知函数f（x）=sin（2x-$\frac{π}{2}$），下列结论错误的是（ ）
| A． | f（x）的最小正周期为π | B． | f（x）在区间$[{0，\frac{π}{2}}]$上是增函数 | ||
| C． | f（x）的图象关于点$（{-\frac{3π}{4}，0}）$对称 | D． | f（x）的图象关于直线$x=\frac{5π}{4}$对称 |
6．“x＞0”是“x2+$\frac{1}{x^2}$≥2”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
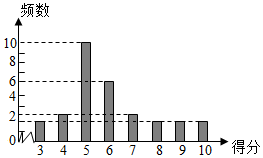为了普及环保知识，增强环保意识，随机抽取某大学30民学生参加环保知识测试，得分（10分制）如图所示，假设得分的中位数为me，众数为mσ，平均数为$\overline{x}$，则me，mσ，$\overline{x}$之间的大小关系是mσ＜me＜$\overline{x}$．