题目内容
11.在△ABC中,内角A,B,C的对边分别为a,b,c,已知2acos2$\frac{C}{2}$+2ccos2$\frac{A}{2}$=3b,且△ABC的周长为6.(1)求b的值;
(2)若B=$\frac{π}{6}$,求△ABC面积的最大值.
分析 (1)根据正弦定理与三角恒等变换,进行化简得出三边成等差数列,再结合周长即可求出b的值;
(2)根据(1)的结论,写出△ABC的面积S=$\frac{1}{2}$acsinB,利用基本不等式即可求出面积的最大值.
解答 解:(1)△ABC中,2acos2$\frac{C}{2}$+2ccos2$\frac{A}{2}$=3b,
由正弦定理得2sinAcos2$\frac{C}{2}$+2sinCcos2$\frac{A}{2}$=3sinB,
即2sinA•$\frac{1+cosC}{2}$+2sinC•$\frac{1+cosA}{2}$=3sinB,
∴sinA+sinC+sinAcosC+cosAsinC=3sinB,
即sinA+sinC+sin(A+C)=3sinB,
∵sin(A+C)=sinB,
∴sinA+sinC=2sinB,
由正弦定理得:a+c=2b;
△ABC的周长为a+b+c=6
∴b=2;
(2)∵B=$\frac{π}{6}$,b=2,∴a+c=4,
∴△ABC的面积为
S=$\frac{1}{2}$acsinB
=$\frac{1}{2}$acsin$\frac{π}{6}$
=$\frac{1}{4}$ac≤$\frac{1}{4}$×${(\frac{a+c}{2})}^{2}$=$\frac{1}{4}$×${(\frac{4}{2})}^{2}$=1,
当且仅当a=c=2时取“=”,
∴△ABC的最大值为1.
点评 本题考查了正弦定理与三角恒等变换的应用问题,也考查了等差数列与基本不等式的应用问题,是综合性题目.

练习册系列答案
相关题目
1.已知函数g(x)=f(x)-x是偶函数,且f(3)=4,则f(-3)=( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |
3.设全集为R,函数f(x)=$\sqrt{{{log}_2}x-1}$的定义域为M,则∁RM=( )
| A. | (-∞,1) | B. | [2,+∞) | C. | (-∞,2) | D. | (0,2) |
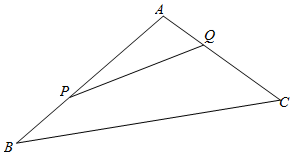 如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.
如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.