题目内容
6.“x>0”是“x2+$\frac{1}{x^2}$≥2”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据基本不等式的性质结合充分条件和必要条件的定义进行判断即可.
解答 解:当x>0时,x2+$\frac{1}{x^2}$≥2成立,即充分性成立,
当x≠0时,由x2+$\frac{1}{x^2}$≥2成立,得x>0或x<0,即x>0不成立,即必要性不成立,
即“x>0”是“x2+$\frac{1}{x^2}$≥2”的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,根据基本不等式的性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知集合M=$\{x|\frac{2-x}{x+1}≥0\}$,N={y|y=lnx},则M∩N=( )
| A. | (0,2] | B. | (-1,2] | C. | (-1,+∞) | D. | R |
14.在△ABC中,知cosA=$\frac{c}{a}$cosC,b+c=2+$\sqrt{2}$,cosB=$\frac{3}{4}$,则△ABC的面积是$\frac{\sqrt{7}}{2}$.
1.已知函数g(x)=f(x)-x是偶函数,且f(3)=4,则f(-3)=( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |
18.已知甲、乙、丙三种食物的维生素及成本入戏表实数:
某学校食堂欲将这三种食物混合加工成100kg混合食物,且要求混合食物中至少需要含35000单位的维生素C及40000单位的维生素D.
(1)设所用食物甲、乙、丙的质量分别为xkg,ykg,100-x-ykg(x≥0,y≥0),试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)用x,y表示这100kg混合食物的成本z,求出z的最小值.
| 食物类型 | 甲 | 乙 | 丙 |
| 维生素C(单位/kg) | 300 | 500 | 300 |
| 维生素D(单位/kg) | 700 | 100 | 300 |
| 成本(元/kg) | 5 | 4 | 3 |
(1)设所用食物甲、乙、丙的质量分别为xkg,ykg,100-x-ykg(x≥0,y≥0),试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)用x,y表示这100kg混合食物的成本z,求出z的最小值.
15.函数y=x+lnx2的大致图象为( )
| A. |  | B. |  | ||
| C. |  | D. |  |
 如图所示,扇形AOB中,圆心角AOB的大小等于$\frac{π}{3}$,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
如图所示,扇形AOB中,圆心角AOB的大小等于$\frac{π}{3}$,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.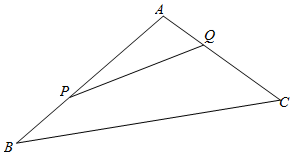 如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.
如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.