题目内容
15.l1过点A(m,1),B(-3,4),l2过点C(0,2),D(1,1),且l1∥l2,则m=0.分析 由已知点的坐标求出两直线的斜率,再由斜率相等求得m值.
解答 解:由l1过点A(m,1),B(-3,4),l2过点C(0,2),D(1,1),且l1∥l2,
可知m≠-3,则${k}_{{l}_{1}}=\frac{4-1}{-3-m}=\frac{3}{-3-m},{k}_{{l}_{2}}=\frac{1-2}{1-0}=-1$,
∴$\frac{3}{-3-m}=-1$,解得m=0.
故答案为:0.
点评 本题考查直线的斜率,考查了直线平行与斜率的关系,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知数列{an}为正项等差数列,满足$\frac{1}{{a}_{1}}$+$\frac{4}{{a}_{2k-1}}$≤1(其中k∈N*,且k≥2),则ak的最小值为$\frac{9}{2}$.
10.设集合A={(x,y)|x2+y2=16,x∈Z,y∈Z},则集合A的子集个数为( )
| A. | 8 | B. | 32 | C. | 16 | D. | 15 |
3.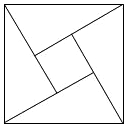 在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
 在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )| A. | 1 | B. | -$\frac{7}{25}$ | C. | $\frac{7}{25}$ | D. | -$\frac{24}{25}$ |
20.在△ABC中,内角A、B、C所对的边为a、b、c,若c2≤a2+b2-ab,则C的取值范围为( )
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{6}$,π) | C. | [$\frac{π}{3}$,π) | D. | (0,$\frac{π}{6}$] |
1.已知函数g(x)=f(x)-x是偶函数,且f(3)=4,则f(-3)=( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |