题目内容
12.△ABC的三内角A,B,C所对边长分别是a,b,c,若$\frac{sinB-sinA}{sinC}$=$\frac{{\sqrt{3}a+c}}{a+b}$,则角B的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
分析 利用正弦定理化简已知可得c2+a2-b2=-$\sqrt{3}$ac,由余弦定理可得cosB=-$\frac{\sqrt{3}}{2}$,结合范围B∈(0,π),即可解得B的值.
解答 解:在△ABC中,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$,可得:sinB=$\frac{b}{2R}$,sinA=$\frac{a}{2R}$,sinC=$\frac{c}{2R}$,
∵$\frac{sinB-sinA}{sinC}$=$\frac{{\sqrt{3}a+c}}{a+b}$,可得:$\frac{b-a}{c}$=$\frac{{\sqrt{3}a+c}}{a+b}$,整理可得:c2+a2-b2=-$\sqrt{3}$ac,
∴由余弦定理可得:cosB=$\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2ac}$=-$\frac{\sqrt{3}}{2}$,
∵B∈(0,π),
∴B=$\frac{5π}{6}$.
故选:B.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
3.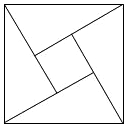 在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
 在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )
在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是$\frac{1}{25}$,则sin2θ-cos2θ的值等于( )| A. | 1 | B. | -$\frac{7}{25}$ | C. | $\frac{7}{25}$ | D. | -$\frac{24}{25}$ |
20.在△ABC中,内角A、B、C所对的边为a、b、c,若c2≤a2+b2-ab,则C的取值范围为( )
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{6}$,π) | C. | [$\frac{π}{3}$,π) | D. | (0,$\frac{π}{6}$] |
17.已知集合M=$\{x|\frac{2-x}{x+1}≥0\}$,N={y|y=lnx},则M∩N=( )
| A. | (0,2] | B. | (-1,2] | C. | (-1,+∞) | D. | R |
1.已知函数g(x)=f(x)-x是偶函数,且f(3)=4,则f(-3)=( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |