题目内容
9．f（x）=xcosx，f（x）=cos（2π-x）-x3sinx的奇偶性分别为奇函数；偶函数．分析 利用奇偶函数的定义分别判断f（-x）与f（x）的关系，在定义域关于原点对称的前提下，如果相等即为偶函数，相反为奇函数．
解答 解：两个函数的定义域为R；
因为f（-x）=-xcos（-x）=-xcosx=-f（x），所以为奇函数；
f（-x）=cos（2π+x）-（-x）3sin（-x）=cosx-x3sinx=f（x），所以为偶函数；
故答案为：奇函数；偶函数．
点评 本题考查了函数奇偶性的判定；首先判断定义域是否关于原点对称；在定义域关于原点对称的前提下，如果相等即为偶函数，相反为奇函数．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
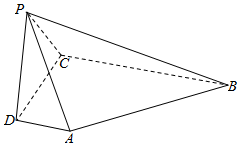如图，在四棱锥P-ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．
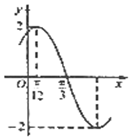已知函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示，下列说法正确的有（ ）个