题目内容
17.(3-x)n的展开式中各项系数和为64,则x3的系数为-540(用数字填写答案)分析 令x=1,则2n=64,解得n=6.再利用通项公式即可得出.
解答 解:令x=1,则2n=64,解得n=6.
(3-x)6的通项公式为:Tr+1=${∁}_{6}^{r}×{3}^{6-r}(-x)^{r}$=(-1)r${∁}_{6}^{r}$•36-r•xr,
令r=3,则x3的系数为-${∁}_{6}^{3}×{3}^{3}$=-540.
故答案为:-540.
点评 本题考查了二项式定理的性质及其通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.已知集合A={1,2},则A的真子集的个数为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
8.等比数列{an}的各项均为正数,且a5a6+a2a9=18,则log3a1+log3a2+…+log3a10的值为( )
| A. | 12 | B. | 10 | C. | 8 | D. | 2+log35 |
9.已知F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,椭圆C上存在点P使∠F1PF2为钝角,则椭圆C的离心率的取值范围是( )
| A. | ($\frac{\sqrt{2}}{2}$,1) | B. | ($\frac{1}{2}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | (0,$\frac{1}{2}$) |
6.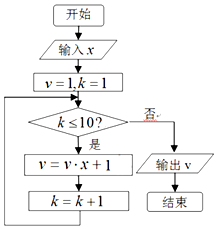 秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为 2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为 2,则输出v的值为( )
 秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为 2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为 2,则输出v的值为( )| A. | 211-1 | B. | 211-2 | C. | 210-1 | D. | 210-2 |
 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.