题目内容
4.从某班5名男生和4名女生中选4人代表班级参加辩论赛,问(1)4人中至少有一名男生的选法有多少种?
(2)若男生甲和女生乙只能有一人参赛且必然有一人参赛,有多少种选法?
(3)辩论队员分为一辩,二辩,三辩,四辩,该班有多少种出赛阵容?
(4)若男生甲和女生乙两人分担当一辩或四辩,则该班有多少种出赛阵容?
分析 (1)间接法,先从9人选4人的种数,再排除全是女生的种数,问题得以解决;
(2)先从男生甲和女生乙选择一个,再从剩下的7人任选3人,问题得以解决;
(3)从9人选4人,并分别安排为一辩,二辩,三辩,四辩,问题得以解决;
(4)男生甲和女生乙两人分担当一辩或四辩,再从剩下的7人任选2人安排二辩,三辩,问题得以解决.
解答 解:(1):间接法:先从9人选4人的种数,再排除全是女生的种数,故有C94-C44=125种,
(2):先从男生甲和女生乙选择一个,再从剩下的7人任选3人,故有C21C73=70种,
(3):从9人选4人,并分别安排为一辩,二辩,三辩,四辩,故有A94=3024种,
(4)男生甲和女生乙两人分担当一辩或四辩,再从剩下的7人任选2人安排二辩,三辩,故有A22A72=84种.
点评 本题考查组合知识,分清是排列还是组合,属于基础题.

练习册系列答案
相关题目
14.定义在R上的函数f(x)=$\frac{xsin2x}{{x}^{2}+a}$的图象如图所示,则实数a的可能值为( )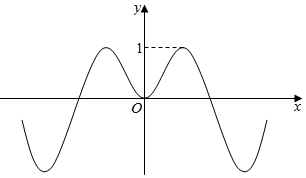

| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
15.已知集合A={x|x-1|≤2},B={x|0<x<2},则A∪B=( )
| A. | A | B. | B | C. | ∅ | D. | R |
9.(1+2x)3(1-x)4展开式中x项的系数为( )
| A. | 10 | B. | -10 | C. | 2 | D. | -2 |



