题目内容
9.(1+2x)3(1-x)4展开式中x项的系数为( )| A. | 10 | B. | -10 | C. | 2 | D. | -2 |
分析 分别展开(1+2x)3=1+${∁}_{3}^{1}(2x)$+${∁}_{3}^{2}(2x)^{2}$+…,(1-x)4=$1+{∁}_{4}^{1}(-x)$+${∁}_{4}^{2}(-x)^{2}$+…,即可得出.
解答 解:∵(1+2x)3=1+${∁}_{3}^{1}(2x)$+${∁}_{3}^{2}(2x)^{2}$+…,
(1-x)4=$1+{∁}_{4}^{1}(-x)$+${∁}_{4}^{2}(-x)^{2}$+…,
∴(1+2x)3(1-x)4展开式中x项的系数为$-{∁}_{4}^{1}$+2${∁}_{3}^{1}$=2,
故选:C.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
18.已知$sinα=\frac{{\sqrt{5}}}{5},sin({α-β})=-\frac{{\sqrt{10}}}{10},α,β$均为锐角,则cos2β=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | -1 | C. | 0 | D. | 1 |
19.若命题“?x∈R,2x2+m>4x”是真命题,则m的值可以是.
| A. | $\frac{3}{2}$ | B. | -1 | C. | 1 | D. | $\frac{2}{3}$ |
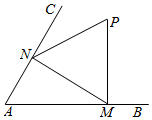 如图,已知∠BAC=$\frac{π}{3}$,正△PMN的顶点M、N分别在射线AB、AC上运动,P在∠BAC的内部,MN=2,M、P、N按逆时针方向排列,设∠AMN=θ.
如图,已知∠BAC=$\frac{π}{3}$,正△PMN的顶点M、N分别在射线AB、AC上运动,P在∠BAC的内部,MN=2,M、P、N按逆时针方向排列,设∠AMN=θ.