题目内容
12.对任意x>0,不等式x+$\frac{1}{x+2a}$>a恒成立,则实数a的取值范围是$[-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}]$.分析 令f(x)=x-a+$\frac{1}{x+2a}$(x>0),f′(x)=$\frac{[x-(-2a-1)][x-(-2a+1)]}{(x+2a)^{2}}$,对a分类讨论,利用导数研究函数的单调性极值与最值即可得出.
解答 解:令f(x)=x-a+$\frac{1}{x+2a}$(x>0),
f′(x)=1-$\frac{1}{(x+2a)^{2}}$=$\frac{[x-(-2a-1)][x-(-2a+1)]}{(x+2a)^{2}}$,
当a≥$\frac{1}{2}$时,0>-2a+1>-2a-1,∴f′(x)>0,此时函数f(x)单调递增,∴f(x)>f(0)=-a+$\frac{1}{2a}$≥0,解得$\frac{1}{2}≤a≤\frac{\sqrt{2}}{2}$.
当$-\frac{1}{2}≤a<\frac{1}{2}$时,-2a+1>0>-2a-1,∴x=-2a+1时,此时函数f(x)取得极小值即最小值,∴f(x)≥f(-2a+1)=-3a+1+1>0,解得$-\frac{1}{2}≤a<\frac{1}{2}$.
当$a<-\frac{1}{2}$时,-2a+1>-2a-1>0,∴函数f(x)在(0,-2a-1)内单调递增,在(-2a-1,-2a+1)内单调递减,在(-2a+1,+∞)内单调递增.
∴必有$\left\{\begin{array}{l}{f(0)=-a+\frac{1}{2a}≥0}\\{f(-2a+1)≥0}\end{array}\right.$,解得$-\frac{\sqrt{2}}{2}$≤a$<-\frac{1}{2}$.
综上可得:实数a的取值范围是$[-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}]$.
故答案为:$[-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}]$.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了分类讨论方法、推理能力与计算能力,属于难题.

| A. | $C_{2016}^k{2^{2016-k}}{5^{k-1}}$ | B. | $C_{2016}^{k-1}{2^{2017-k}}{5^{k-1}}$ | ||
| C. | $C_{2016}^{k-1}$ | D. | $C_{2016}^k{2^{2016-k}}{5^k}$ |
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | -1 | C. | 0 | D. | 1 |
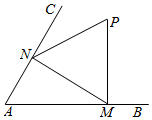 如图,已知∠BAC=$\frac{π}{3}$,正△PMN的顶点M、N分别在射线AB、AC上运动,P在∠BAC的内部,MN=2,M、P、N按逆时针方向排列,设∠AMN=θ.
如图,已知∠BAC=$\frac{π}{3}$,正△PMN的顶点M、N分别在射线AB、AC上运动,P在∠BAC的内部,MN=2,M、P、N按逆时针方向排列,设∠AMN=θ.