题目内容
14．定义在R上的函数f（x）=$\frac{xsin2x}{{x}^{2}+a}$的图象如图所示，则实数a的可能值为（ ）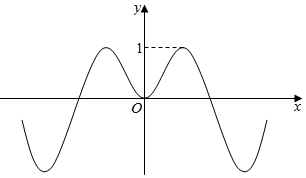
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | 1 |
分析 由题意可知，当x＞0时存在x使$\frac{xsin2x}{{x}^{2}+a}$=1成立，根据三角形函数的图象和性质即可基本不等式求出a＜$\frac{1}{4}$，即可判断选项．
解答 解：由图象可知，当x＞0时存在x使$\frac{xsin2x}{{x}^{2}+a}$=1成立，
∴xsin2x=x2+a，
∴sin2x=x+$\frac{a}{x}$，
∵-1≤sin2x≤1，
∴-1≤x+$\frac{a}{x}$≤1，
∵x+$\frac{a}{x}$≥$2\sqrt{x•\frac{a}{x}}$=2$\sqrt{a}$，当且仅当x=$\sqrt{a}$时取等号，
∴2$\sqrt{a}$＜1，
∴a＜$\frac{1}{4}$，
故选：A．
点评 本题考查了函数图象和性质以及基本不等式的应用，属于中档题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
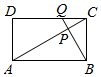如图，在矩形ABCD中，AB=$\sqrt{3}$AD，点Q为线段CD（含端点）上一个动点，且$\overrightarrow{DQ}$=λ$\overrightarrow{QC}$，BQ交AC于P，且$\overrightarrow{AP}$=μ$\overrightarrow{PC}$，若AC⊥BP，则λ-μ=-1．
6．若函数f（x）=2sin2x的图象向右平移φ（0＜φ＜π）个单位后得到函数g（x）的图象，若对满足|f（x1）-g（x2）|=4的x1、x2，有|x1-x2|的最小值为$\frac{π}{6}$，则φ=（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$或$\frac{2π}{3}$ | D． | $\frac{π}{6}$或$\frac{5π}{6}$ |
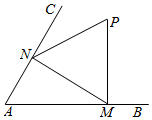如图，已知∠BAC=$\frac{π}{3}$，正△PMN的顶点M、N分别在射线AB、AC上运动，P在∠BAC的内部，MN=2，M、P、N按逆时针方向排列，设∠AMN=θ．