题目内容
为了研究男羽毛球运动员的身高x(单位:cm)与体重y(单位:kg)的关系,通过随机抽样的方法抽取5名运动员,测得他们的身高和体重的关系如下表:
从这5人中随机抽取2人,将他们的体重作为一个样本,则该样本的平均数与总体中体重的平均数之差的绝对值不超过1的概率为 .
| 身高(x) | 172 | 174 | 176 | 178 | 180 |
| 体重(y) | 74 | 73 | 76 | 75 | 77 |
考点:列举法计算基本事件数及事件发生的概率,分层抽样方法
专题:概率与统计
分析:由表格中的数据和平均数公式求出体重的平均数,利用体重列出所有的基本事件,找出满足条件的基本事件,代入概率公式求值.
解答:
解:由表格中的数据得,平均数
=
=75,
从这5人中抽取的2个人的体重为:
(74,73),(74,76),(74,75),(74,77);
(73,76),(73,75),(73,77);
(76,75),(76,77);
(75,77),共有10中情况.
满足条件的有:(74,76),(74,75),(74,77)(73,76),(73,75),
(73,77),(75,77),共7种情况,
所以所求的概率P=
,
故答案为:
.
. |
| y |
| 74+73+76+75+77 |
| 5 |
从这5人中抽取的2个人的体重为:
(74,73),(74,76),(74,75),(74,77);
(73,76),(73,75),(73,77);
(76,75),(76,77);
(75,77),共有10中情况.
满足条件的有:(74,76),(74,75),(74,77)(73,76),(73,75),
(73,77),(75,77),共7种情况,
所以所求的概率P=
| 7 |
| 10 |
故答案为:
| 7 |
| 10 |
点评:本题考查古典概型下的概率公式,以及列举法求基本事件的个数,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若直线y=kx-k交抛物线y2=4x于A,B两点,且线段AB中点到y轴的距离为3,则|AB|=( )
| A、12 | B、10 | C、8 | D、6 |
直线m与平面α平行的充要条件是( )
| A、直线m与平面α没有公共点 |
| B、直线m与平面α内的一条直线平行 |
| C、直线m与平面α内的无数条直线平行 |
| D、直线m与平面α内的任意一条直线平行 |
二次函数y=x2+px+q的零点为1和m,且-1<m<0,那么p,q应满足的条件是( )
| A、p>0且p<0 |
| B、p>0且p>0 |
| C、p<0且p>0 |
| D、p<0且p<0 |
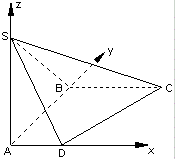 已知ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=