题目内容

7．已知e是自然对数的底数，函数f（x）=ex+x-2的零点为a，函数g（x）=lnx+x-2的零点为b，则下列不等式中成立的是（　　）
A．a＜1＜bB．a＜b＜1C．1＜a＜bD．b＜1＜a

分析 根据函数与方程之间的关系转化为函数y=ex与y=2-x，y=lnx与y=2-x交点的横坐标的大小问题，利用数形结合进行比较即可．

解答 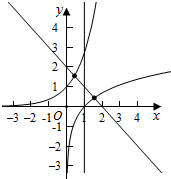解：由f（x）=ex+x-2=0得ex=2-x，
由g（x）=lnx+x-2=0得lnx=2-x，
作出计算y=ex，y=lnx，y=2-x的图象如图：
∵函数f（x）=ex+x-2的零点为a，函数g（x）=lnx+x-2的零点为b，
∴y=ex与y=2-x的交点的横坐标为a，y=lnx与y=2-x交点的横坐标为b，
由图象知a＜1＜b，
故选：A．

点评 本题主要考查函数与方程的应用，利用函数转化为两个图象的交点问题，结合数形结合是解决本题的关键．

练习册系列答案
相关题目
17．已知F1（-c，0），F2（c，0）分别是椭圆M：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，且|F1F2|=2$\sqrt{3}$，离心率e=$\frac{\sqrt{3}}{2}$．（1）求椭圆M的标准方程；
（2）过椭圆右焦点F2作直线l交椭圆M于A，B两点．
①当直线l的斜率为1时，求线段AB的长；
②若椭圆M上存在点P，使得以OA，OB为邻边的四边形OAPB为平行四边形（O为坐标原点），求直线l的方程．
18．在一次跳高比赛前，甲、乙两名运动员各试跳了一次．设命题p表示“甲的试跳成绩超过2米”，命题q表示“乙的试跳成绩超过2米”，则命题p∨q表示（　　）
A．甲、乙恰有一人的试跳成绩没有超过2米
B．甲、乙至少有一人的试跳成绩没有超过2米
C．甲、乙两人的试跳成绩都没有超过2米
D．甲、乙至少有一人的试跳成绩超过2米
15．将十进制数2016（10）化为八进制数为3740（8）．
2．椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的左，右焦点分别为F1（-1，0），F2（1，0），点P为椭圆上任意一点，且△PF1F2的内切圆面积的最大值为$\frac{1}{3}$π．
（Ⅰ）求椭圆C的方程；
（Ⅱ）直线l：y=kx+b（k＞0，b＞0）是圆O：x2+y2=3的一条切线，且l与椭圆C交于不同的两点A，B．若弦AB的长为$\frac{4\sqrt{6}}{7}$，求直线l的方程．
12．已知函数f（x）=2|x-2|+ax（x∈R）．
（1）当a=1时，求f（x）的最小值；
（2）当f（x）有最小值时，求a的取值范围；
（3）若函数h（x）=f（sinx）-2存在零点，求a的取值范围．
19．某市政府为了确定一个较为合理的居民用电标准，必须先了解全市  居民日常用电量的分布情况．现采用抽样调查的方式，获得了n位居民在2015年的月均用电量（单位：度）数据，样本统计结果如图表：
（1）求n的值和月均用电量的平均数估计值；
（2）如果用分层抽样的方法从用电量小于30度的居民中抽取5位居民，再从这5位居民中选2人，那么至少有1位居民月均用电量在20至30度的概率是多少？
分组频数频率
[0，10）0.05
[10，20）0.10
[20，30）30
[30，40）0.25
[40，50）0.15
[50，60]15
合计n1
16．过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$中心的直线交椭圆于A，B两点，右焦点为F2（c，0），则△ABF2的最大面积为（　　）
A．b2B．abC．acD．bc
17．若圆x2+y2+2x-4y=0关于直线3x+y+m=0对称，则实数m的值为（　　）
A．-3B．-1C．1D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网