题目内容

17．已知F1（-c，0），F2（c，0）分别是椭圆M：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，且|F1F2|=2$\sqrt{3}$，离心率e=$\frac{\sqrt{3}}{2}$．（1）求椭圆M的标准方程；
（2）过椭圆右焦点F2作直线l交椭圆M于A，B两点．
①当直线l的斜率为1时，求线段AB的长；
②若椭圆M上存在点P，使得以OA，OB为邻边的四边形OAPB为平行四边形（O为坐标原点），求直线l的方程．

分析 （1）运用离心率公式和a，b，c的关系，可得a，b，进而得到椭圆方程；
（2）①设直线l：y=x-$\sqrt{3}$，代入椭圆方程，求出方程的根，即可求线段AB的长；
②假设椭圆上存在点P（m，n），使得以OA、OB为邻边的四边形OAPB为平行四边形．设直线方程为y=k（x-$\sqrt{3}$），代入椭圆方程，运用韦达定理，结合$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$，则m=x1+x2，n=y1+y2，求得P的坐标，代入椭圆方程，即可得到k，即可判断P的存在和直线的方程．

解答 解：（1）由题意，2c=2$\sqrt{3}$，得$c=\sqrt{3}$，
又$\frac{c}{a}=\frac{\sqrt{3}}{2}$，∴a=2，b2=a2-c2=1，
∴椭圆M的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$；
（2）①可设直线方程为y=x-$\sqrt{3}$代入椭圆方程可得5x2-8$\sqrt{3}$x+8=0，
∴x=$\frac{4\sqrt{3}±2\sqrt{2}}{5}$，∴弦AB的长为$\sqrt{2}×\frac{4\sqrt{2}}{5}=\frac{8}{5}$；
②假设椭圆上存在点P（m，n），使得以OA、OB为邻边的四边形OAPB为平行四边形．
设直线方程为y=k（x-$\sqrt{3}$），代入椭圆方程，可得（1+4k2）x2-8$\sqrt{3}$k2x+12k2-4=0，
设A（x1，y1），B（x2，y2），
由$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$，则m=x1+x2，n=y1+y2，
x1+x2=$\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$，x1x2=$\frac{12{k}^{2}-4}{1+4{k}^{2}}$，
y1+y2=k（x1+x2-2$\sqrt{3}$）=k（$\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$-2$\sqrt{3}$）=$\frac{-2\sqrt{3}}{1+4{k}^{2}}$，
即有P（$\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$，$\frac{-2\sqrt{3}}{1+4{k}^{2}}$），
代入椭圆方程可得$\frac{48{k}^{4}}{（1+4{k}^{2}）^{2}}+\frac{12{k}^{2}}{（1+4{k}^{2}）^{2}}=1$，
解得k2=$\frac{1}{8}$，即k=±$\frac{\sqrt{2}}{4}$，
故存在点P（$\frac{\sqrt{3}}{3}，-\frac{\sqrt{6}}{6}$），或（$\frac{\sqrt{3}}{3}，\frac{\sqrt{6}}{6}$），
则有直线l：y=$\frac{\sqrt{2}}{4}x-\frac{\sqrt{6}}{4}$或y=-$\frac{\sqrt{2}}{4}x+\frac{\sqrt{6}}{4}$．

点评 本题考查椭圆的方程和性质，主要考查离心率公式和方程的运用，联立直线方程，运用韦达定理，考查运算能力，属于中档题

练习册系列答案
相关题目
7．如图，在三棱柱ABC-A1B1C1中，已知AB⊥侧面BB1C1C，AB=BC=1，BB1=2，∠BCC1=$\frac{π}{3}$．
（1）求证：C1B⊥平面ABC；
（2）点B1到平面ACC1A1的距离为d1，点A1到平面ABC1的距离为d2，求$\frac{{d}_{1}}{{d}_{2}}$．
8．已知$|{\begin{array}{l}{cos75°}&{-sinα}\\{sin75°}&{cosα}\end{array}}|=\frac{1}{3}$，则cos（30°+2α）=$\frac{7}{9}$．
5．如图正方体ABCD-A1B1C1D1的棱长为2，线段B1D1上有两个动点E、F，且EF=1，则下列结论中错误的是（　　）
A．EF∥平面ABCDB．AC⊥BE
C．三棱锥A-BEF体积为定值D．△BEF与△AEF面积相等
12．以下表示x轴的参数方程是（　　）
A．$\left\{\begin{array}{l}{x={t}^{2}+1}\\{y=0}\end{array}\right.$（t为参数）B．$\left\{\begin{array}{l}{x=0}\\{y=3t+1}\end{array}\right.$（t为参数）
C．$\left\{\begin{array}{l}{x=1+sinθ}\\{y=0}\end{array}\right.$（θ为参数）D．$\left\{\begin{array}{l}{x=4t+1}\\{y=0}\end{array}\right.$（t为参数）
2．已知F1，F2是椭圆$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1的两个焦点，过点F2的直线交椭圆于M，N两点，在△F1MN中，若有两边之和是14，则第三边的长度为（　　）
A．6B．5C．4D．3
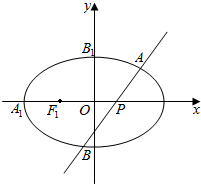9．如图，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1，|A1B1|=$\sqrt{7}$，F1是椭圆C的左焦点，A1是椭圆C的左顶点，B1是椭圆C的上顶点，且$\overrightarrow{{A}_{1}{F}_{1}}$=$\overrightarrow{{F}_{1}O}$，点P（n，0）（n≠0）是长轴上的任一定点，过P点的任一直线l交椭圆C于A，B两点．
（1）求椭圆C的方程；
（2）是否存在定点Q（x0，0），使得$\overrightarrow{QA}$•$\overrightarrow{QB}$为定值，若存在，试求出定点Q的坐标，并求出此定值；若不存在，请说明理由．
6．已知过点（0，-$\sqrt{3}$）的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1（m＞0，n＞0）有相同的焦点（-c，0）和（c，0），若c是a、m的等比中项，n2是2m2与c2的等差中项．
（1）求椭圆的离心率；
（2）设直AB与椭圆交于不同两点A、B，点A关于x轴的对称点为A′，若直线AB过定点T（$\sqrt{2}$，0），求证：直线A′B过定点P（2$\sqrt{2}$，0）．
7．已知e是自然对数的底数，函数f（x）=ex+x-2的零点为a，函数g（x）=lnx+x-2的零点为b，则下列不等式中成立的是（　　）
A．a＜1＜bB．a＜b＜1C．1＜a＜bD．b＜1＜a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网