题目内容
已知等差数列{an}的公差d≠0,a1=1,且a1,a3,a9成等比数列.
(1)求数列{an}的公差d及通项an;
(2)求数列{2an}的前n项和Sn.
(1)求数列{an}的公差d及通项an;
(2)求数列{2an}的前n项和Sn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列的通项公式和等比数列的性质,求出d=1,由此能求出an=n.
(2)由(1)知2am=2n,由此能求出数列{2an}的前n项和Sn.
(2)由(1)知2am=2n,由此能求出数列{2an}的前n项和Sn.
解答:
解:(1)由题设知公差d≠0,
由a1=1,a1,a3,a9成等比数列,
得:
=
,…(3分)
解得d=1,d=0(舍去)…(4分)
故{an}的通项an=1+(n-1)×1=n.…(6分)
(2)由(1)知2am=2n,…(8分)
由等比数列前n项和公式得
Sn=2+22+23+…+2n=
…(11分)
=2n+1-2.…(12分)
由a1=1,a1,a3,a9成等比数列,
得:
| 1+2d |
| 1 |
| 1+8d |
| 1+2d |
解得d=1,d=0(舍去)…(4分)
故{an}的通项an=1+(n-1)×1=n.…(6分)
(2)由(1)知2am=2n,…(8分)
由等比数列前n项和公式得
Sn=2+22+23+…+2n=
| 2(1-2n) |
| 1-2 |
=2n+1-2.…(12分)
点评:本题考查数列的通项公式和前n项和的求法,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.

练习册系列答案
相关题目
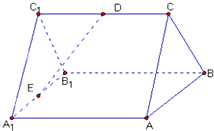 如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点.
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点. 某校高三年段共有1000名学生,将其按专业发展取向分成普理、普文、艺体三类,如图是这三类的人数比例示意图.为开展某项调查,采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本.
某校高三年段共有1000名学生,将其按专业发展取向分成普理、普文、艺体三类,如图是这三类的人数比例示意图.为开展某项调查,采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本.