题目内容
若函数y=
在(m,+∞)上为增函数(m为常数),则称f(x)为区间(m,+∞)上的“一阶比增函数”.
已知函数f(x)是在(0,+∞)上每一点处可导的函数,且xf′(x)>f(x)在(0,+∞)上恒成立.
(1)求证:f(x)为区间(0,+∞)上的“一阶比增函数”;
(2)当x1>0,x2>0时,证明:f(x1)+f(x2)<f(x1+x2);
(3)已知不等式ln(l+x)<x在x>-1且x≠0时恒成立,证明:
ln2+
ln4+…+
ln(n+1)>
(n∈N*).
| f(x) |
| x |
已知函数f(x)是在(0,+∞)上每一点处可导的函数,且xf′(x)>f(x)在(0,+∞)上恒成立.
(1)求证:f(x)为区间(0,+∞)上的“一阶比增函数”;
(2)当x1>0,x2>0时,证明:f(x1)+f(x2)<f(x1+x2);
(3)已知不等式ln(l+x)<x在x>-1且x≠0时恒成立,证明:
| 1 |
| 22 |
| 1 |
| 33 |
| 1 |
| (n+1)2 |
| n |
| 4(n+1)(n+2) |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)由“一阶比增函数”的意义知只需说明y=
在(0,+∞)上是单调增函数.求导可得结论;
(2)由(1)知y=
在(0,+∞)上是单调增函数.当x1>0,x2>0时,
>
,
>
.变形后两式相加可得结论;
(3)由(2)知,n≥2时,可得f(x1)+f(x2)+f(x3)+…+f(xn)<f(x1+x2+x3+…+xn)(n≥2)恒成立.构造f(x)=xlnx,知xf′(x)-f(x)=x(lnx+1)-xlnx=x>0符合条件,则当xi>0(i=1,2,3,…,n)时,有x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+x3+…+xn)ln(x1+x2+x3+…+xn)(n≥2)(*)恒成立.令xn=
,记Sn=x1+x2+…+xn=
+
+…+
,
利用放缩法可得
-
<Sn<1-
,则(x1+x2+x3+…+xn)ln(x1+x2+x3+…+xn)<(x1+x2+x3+…+xn)ln(1-
)<-
(x1+x2+x3+…+xn)(∵ln(1+x)<x),<-
(
-
)=-
(**),再由(**)及(*)可得结论.
| f(x) |
| x |
(2)由(1)知y=
| f(x) |
| x |
| f(x1+x2) |
| x1+x2 |
| f(x1) |
| x1 |
| f(x1+x2) |
| x1+x2 |
| f(x2) |
| x2 |
(3)由(2)知,n≥2时,可得f(x1)+f(x2)+f(x3)+…+f(xn)<f(x1+x2+x3+…+xn)(n≥2)恒成立.构造f(x)=xlnx,知xf′(x)-f(x)=x(lnx+1)-xlnx=x>0符合条件,则当xi>0(i=1,2,3,…,n)时,有x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+x3+…+xn)ln(x1+x2+x3+…+xn)(n≥2)(*)恒成立.令xn=
| 1 |
| (n+1)2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
利用放缩法可得
| 1 |
| 2 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2(n+1)(n+2) |
解答:
证明:(1)由y=
,对y求导知y′=
,
由xf′(x)>f(x)可知:y′>0在(0,+∞)上恒成立.
从而y=
在(0,+∞)上是单调增函数.
∴f(x)为区间(0,+∞)上的“一阶比增函数”.
(2)由(1)知y=
在(0,+∞)上是单调增函数.
当x1>0,x2>0时,
>
,
>
.
于是f(x1)<
f(x1+x2),f(x2)<
f(x1+x2),
两式相加得到:f(x1)+f(x2)<f(x1+x2).
(3)由(2)可知:y=
在(0,+∞)上是单调递增函数,
f(x1)+f(x2)<f(x1+x2)(x1,>0,x2>0)恒成立,
则当n≥2时,f(x1+x2+x3+…+xn)=f[x1+(x2+x3+…+xn)]>f(x1)+f(x2+x3+…+xn)
=f(x1)+f[x2+(x3+…+xn)]>f(x1)+f(x2)+f(x3+…+xn)
=…>f(x1)+f(x2)+f(x3)+…+f(xn)恒成立.即f(x1)+f(x2)+f(x3)+…+f(xn)<f(x1+x2+x3+…+xn)(n≥2)恒成立.
构造f(x)=xlnx,知xf′(x)-f(x)=x(lnx+1)-xlnx=x>0符合条件,
则当xi>0(i=1,2,3,…,n)时,
有x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+x3+…+xn)ln(x1+x2+x3+…+xn)(n≥2)(*)恒成立.
令xn=
,记Sn=x1+x2+…+xn=
+
+…+
,
则Sn<
+
+…+
=1-
+
-
+…+
-
=1-
,
Sn>
+
+…+
=
-
+
-
+…+
-
=
-
,
∴(x1+x2+x3+…+xn)ln(x1+x2+x3+…+xn)<(x1+x2+x3+…+xn)ln(1-
)
<-
(x1+x2+x3+…+xn)(∵ln(1+x)<x),
<-
(
-
)=-
(**),
由(**)及(*)可知:
ln
+
ln
+…+
ln
<-
,
于是
ln22+
ln32+
ln42+…+
ln(n+1)2>
,
ln2+
ln3+…+
ln(n+1)>
(n∈N*)
| f(x) |
| x |
| f′(x)•x-f(x) |
| x2 |
由xf′(x)>f(x)可知:y′>0在(0,+∞)上恒成立.
从而y=
| f(x) |
| x |
∴f(x)为区间(0,+∞)上的“一阶比增函数”.
(2)由(1)知y=
| f(x) |
| x |
当x1>0,x2>0时,
| f(x1+x2) |
| x1+x2 |
| f(x1) |
| x1 |
| f(x1+x2) |
| x1+x2 |
| f(x2) |
| x2 |
于是f(x1)<
| x1 |
| x1+x2 |
| x2 |
| x1+x2 |
两式相加得到:f(x1)+f(x2)<f(x1+x2).
(3)由(2)可知:y=
| f(x) |
| x |
f(x1)+f(x2)<f(x1+x2)(x1,>0,x2>0)恒成立,
则当n≥2时,f(x1+x2+x3+…+xn)=f[x1+(x2+x3+…+xn)]>f(x1)+f(x2+x3+…+xn)
=f(x1)+f[x2+(x3+…+xn)]>f(x1)+f(x2)+f(x3+…+xn)
=…>f(x1)+f(x2)+f(x3)+…+f(xn)恒成立.即f(x1)+f(x2)+f(x3)+…+f(xn)<f(x1+x2+x3+…+xn)(n≥2)恒成立.
构造f(x)=xlnx,知xf′(x)-f(x)=x(lnx+1)-xlnx=x>0符合条件,
则当xi>0(i=1,2,3,…,n)时,
有x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+x3+…+xn)ln(x1+x2+x3+…+xn)(n≥2)(*)恒成立.
令xn=
| 1 |
| (n+1)2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
则Sn<
| 1 |
| 1•2 |
| 1 |
| 2•3 |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
Sn>
| 1 |
| 2•3 |
| 1 |
| 3•4 |
| 1 |
| (n+1)(n+2) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
∴(x1+x2+x3+…+xn)ln(x1+x2+x3+…+xn)<(x1+x2+x3+…+xn)ln(1-
| 1 |
| n+1 |
<-
| 1 |
| n+1 |
<-
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2(n+1)(n+2) |
由(**)及(*)可知:
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
| 1 |
| (n+1)2 |
| n |
| 2(n+1)(n+2) |
于是
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| (n+1)2 |
| n |
| 2(n+1)(n+2) |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
| n |
| 4(n+1)(n+2) |
点评:该题考查利用导数研究函数的单调性、最值及不等式的证明,考查学生的推理论证能力、运算求解能力,考查学生综合运用所学知识分析解决问题的能力,该题综合性强,运算量大,能力要求高.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
定义在R上的可导函数f(x),当x∈(1,+∞)时,(x-1)f′(x)-f(x)>0恒成立,a=f(2),b=
f(3),c=(
+1)f(
),则a、b、c的大小关系为( )
| 1 |
| 2 |
| 2 |
| 2 |
| A、c<a<b |
| B、b<c<a |
| C、a<c<b |
| D、c<b<a |
 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.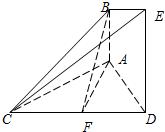 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.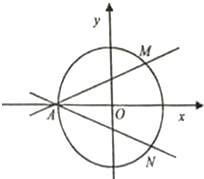 如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.
如图,在直角坐标系xOy中,圆O:x2+y2=4与x轴负半轴交于点A,过点A的直线AM,AN分别与圆O交于M,N两点.