题目内容
函数f(x)定义域为I,存在非零常数T,对于任意的x∈I,都有f(x+T)=-f(x),则f(x)是周期函数吗?若都有f(x+T)=
,则f(x)是周期函数吗?若都有f(x+T)=-
,则f(x)是周期函数吗?请给出详细的证明.
| 1 |
| f(x) |
| 1 |
| f(x) |
考点:函数的周期性
专题:函数的性质及应用
分析:根据周期函数的定义,若f(x+T)=f(x)则f(x)为周期函数,其中T为非零常数.
解答:
(1)∵f(x+T)=-f(x),
∴f(x+2T)=-f(x+T)=-[-f(x)]=f(x)
即存在非零常数2T,对于任意的x∈I;都有
f(x+2T)=f(x),
∴f(x)是以2T为周期的周期函数.
(2)∵f(x+T)=
,
∴f(x+2T)=f(x+T+T)=
=
=f(x),
即存在非零常数2T,对于任意的x∈I,都有f(x+2T)=f(x),
∴f(x)是以2T为周期的周期函数.
(3)∵f(x+T)=-
,
∴f(x+2T)=-
=-
=f(x),
即存在非零常数2T,对于任意的x∈I;都有
f(x+2T)=f(x),
∴f(x)是以2T为周期的周期函数.
∴f(x+2T)=-f(x+T)=-[-f(x)]=f(x)
即存在非零常数2T,对于任意的x∈I;都有
f(x+2T)=f(x),
∴f(x)是以2T为周期的周期函数.
(2)∵f(x+T)=
| 1 |
| f(x) |
∴f(x+2T)=f(x+T+T)=
| 1 |
| f(x+T) |
| 1 | ||
|
即存在非零常数2T,对于任意的x∈I,都有f(x+2T)=f(x),
∴f(x)是以2T为周期的周期函数.
(3)∵f(x+T)=-
| 1 |
| f(x) |
∴f(x+2T)=-
| 1 |
| f(x+T) |
| 1 | ||
-
|
即存在非零常数2T,对于任意的x∈I;都有
f(x+2T)=f(x),
∴f(x)是以2T为周期的周期函数.
点评:本题主要考查了周期函数的定义以及转化思想.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知等差数列{an}中,其前n项的和为Sn,a3+a5=8,且S9=45,则a2014=( )
| A、1006 | B、1007 |
| C、2013 | D、2014 |
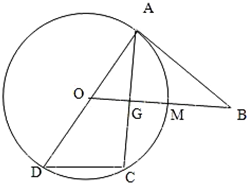 如图所示,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12,则BM=
如图所示,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12,则BM=