题目内容
已知某几何体的三视图如图所示，求它的表面积和体积．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：先判断三视图复原的几何体的形状，结合三视图的数据，确定正方体的棱长及圆锥的底面半径和高及母线长，可得几何体的表面积和体积．
解答：
解：由已知中的三视图可得该几何体是一个正方体挖去一个圆锥后的组合体，
正方体的棱长为2，
故正方体的体积为：8，
圆锥的底面半径为1，高为2，
故圆锥的体积为：
×π×2=
，
故组合体的体积V=8-
，
圆锥的母线长为：
=
，
故组合体的表面积S=6×22-π+
π=24-π+
π
正方体的棱长为2，
故正方体的体积为：8，
圆锥的底面半径为1，高为2，
故圆锥的体积为：
| 1 |
| 3 |
| 2π |
| 3 |
故组合体的体积V=8-
| 2π |
| 3 |
圆锥的母线长为：
| 22+12 |
| 5 |
故组合体的表面积S=6×22-π+
| 5 |
| 5 |
点评：本题考查由三视图求几何体的侧面积和体积，考查空间想象能力，是基础题．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
相关题目
下面命题正确的个数是（ ）
（1）若直线l上有无数个点不在平面α内，则l∥α；
（2）若直线l平行于平面α内的无数条直线，则l∥α；
（3）若直线l与平面α平行，则l与平面α内的任一直线平行；
（4）若直线l在平面α外，则l∥α．
（1）若直线l上有无数个点不在平面α内，则l∥α；
（2）若直线l平行于平面α内的无数条直线，则l∥α；
（3）若直线l与平面α平行，则l与平面α内的任一直线平行；
（4）若直线l在平面α外，则l∥α．
| A、0个 | B、1个 | C、2个 | D、3个 |
椭圆
+
=1的一个焦点坐标是（ ）
| x2 |
| 3 |
| y2 |
| 4 |
| A、（1，0） |
| B、（0，1） |
| C、（0，7） |
| D、（7，0） |
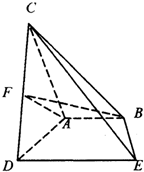如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．