题目内容
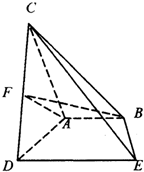 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求三棱锥A-BCF的体积.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
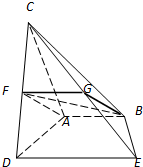
分析:(1)取CE的中点G,连结FG、BG.由已知条件推导出四边形GFAB为平行四边形,由此能证明AF∥平面BCE.
(2)由等边三角形性质得AF⊥CD,由线面垂直得DE⊥AF,从而AF⊥平面CDE,由平行线性质得BG⊥平面CDE,由此能证明平面BCE⊥平面CDE.
(3)由已知条件利用等积法能求出三棱锥A-BCF的体积.
(2)由等边三角形性质得AF⊥CD,由线面垂直得DE⊥AF,从而AF⊥平面CDE,由平行线性质得BG⊥平面CDE,由此能证明平面BCE⊥平面CDE.
(3)由已知条件利用等积法能求出三棱锥A-BCF的体积.
解答:
 (本小题满分14分)
(本小题满分14分)
(1)证明:取CE的中点G,连结FG、BG. …(1分)
∵F为CD的中点,
∴GF∥DE且GF=
DE.
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB. …(2分)
又AB=
DE,∴GF=AB. …(3分)
∴四边形GFAB为平行四边形,
则AF∥BG.…(4分)
∵AF不包含于平面BCE,BG?平面BCE,
∴AF∥平面BCE. …(5分)
(2)证明:∵△ACD为等边三角形,F为CD的中点,∴AF⊥CD.…(6分)
∵DE⊥平面ACD,AF?平面ACD,∴DE⊥AF. …(7分)
又CD∩DE=D,故AF⊥平面CDE.…(8分)
∵BG∥AF,∴BG⊥平面CDE.
∵BG?平面BCE,∴平面BCE⊥平面CDE. …(10分)
(3)解:∵AB⊥平面ACD,∴AB是三棱锥B-ACF的高.…(11分)
∵△ACD为等边三角形,且AD=DE=2AB=2,∴AB=1.…(12分)
∴VA-BCF=VACF=
×S△ACF×AB …(13分)
=
×
×S△ACD×AB
=
×
×
×22×1
=
.…(14分)
 (本小题满分14分)
(本小题满分14分)(1)证明:取CE的中点G,连结FG、BG. …(1分)
∵F为CD的中点,
∴GF∥DE且GF=
| 1 |
| 2 |
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB. …(2分)
又AB=
| 1 |
| 2 |
∴四边形GFAB为平行四边形,
则AF∥BG.…(4分)
∵AF不包含于平面BCE,BG?平面BCE,
∴AF∥平面BCE. …(5分)
(2)证明:∵△ACD为等边三角形,F为CD的中点,∴AF⊥CD.…(6分)
∵DE⊥平面ACD,AF?平面ACD,∴DE⊥AF. …(7分)
又CD∩DE=D,故AF⊥平面CDE.…(8分)
∵BG∥AF,∴BG⊥平面CDE.
∵BG?平面BCE,∴平面BCE⊥平面CDE. …(10分)
(3)解:∵AB⊥平面ACD,∴AB是三棱锥B-ACF的高.…(11分)
∵△ACD为等边三角形,且AD=DE=2AB=2,∴AB=1.…(12分)
∴VA-BCF=VACF=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
=
| ||
| 6 |
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 从1开始的自然数按如图所示的规则排列,现有一个三角形框架在图中上下或左右移动,使每次恰有九个数在此三角形内,则这九个数的和可以为( )
从1开始的自然数按如图所示的规则排列,现有一个三角形框架在图中上下或左右移动,使每次恰有九个数在此三角形内,则这九个数的和可以为( )| A、2097 | B、1553 |
| C、1517 | D、2111 |
椭圆
+
=1的焦点坐标为( )
| y2 |
| 13 |
| x2 |
| 4 |
| A、(±2,0) |
| B、(±3,0) |
| C、(0,±2) |
| D、(0,±3) |

 如图,ABCD和ABEF都是正方形,M∈AC,N∈FB,且AM=FN.证明:MN∥平面BCE.
如图,ABCD和ABEF都是正方形,M∈AC,N∈FB,且AM=FN.证明:MN∥平面BCE.