题目内容
1.正三角形ABC的边长为1,设$\overrightarrow{AB}$=$\vec a$,$\overrightarrow{BC}$=$\vec b$,$\overrightarrow{AC}$=$\vec c$,那么$\vec a$•$\vec b$+$\vec b$•$\vec c$+$\vec c$•$\vec a$的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
分析 由题意可知向量:|$\vec a$|=|$\vec b$|=|$\vec c$|=1,然后直接代入向量的数量积公式计算
解答 解:由题意可知:|$\vec a$|=|$\vec b$|=|$\vec c$|=1,
那么$\vec a$•$\vec b$+$\vec b$•$\vec c$+$\vec c$•$\vec a$=|$\vec a$|•|$\vec b$|+|$\vec b$|•|$\vec c$|+|$\vec c$|•|$\vec a$|=1•1•cos120°+1•1•cos60°+1•1•cos60°=-$\frac{1}{2}$+$\frac{1}{2}$+$\frac{1}{2}$=$\frac{1}{2}$,
故选:C.
点评 本题考查了平面向量的数量积运算,解答的关键是熟记公式及注意向量的夹角,是基础题.

练习册系列答案
相关题目
9.函数f(x)=$\sqrt{1-x}$-$\sqrt{x}$的定义域为( )
| A. | [0,1] | B. | (0,1] | C. | (0,1) | D. | (-1,0) |
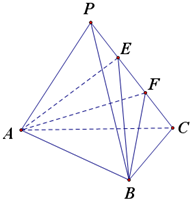 在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.
在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.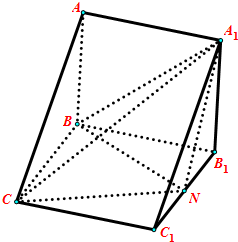 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.