题目内容
7.已知角α(-π≤α<π)的终边过点P(sin$\frac{2π}{3}$,cos$\frac{2π}{3}$),则α=$-\frac{π}{6}$.分析 利用角α(-π≤α<π)的终边过点P(sin$\frac{2π}{3}$,cos$\frac{2π}{3}$),tanα=-$\frac{\sqrt{3}}{3}$(-π≤α<π),且P在第四象限,即可得出结论.
解答 解:∵角α(-π≤α<π)的终边过点P(sin$\frac{2π}{3}$,cos$\frac{2π}{3}$),
∴tanα=-$\frac{\sqrt{3}}{3}$(-π≤α<π),
∵sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$>0,cos$\frac{2π}{3}$=-$\frac{1}{2}$<0,
∴P在第四象限,
∴α=$-\frac{π}{6}$.
故答案为:$-\frac{π}{6}$.
点评 本题重点考查三角函数的定义,考查学生的计算能力,正确运用公式是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
18.已知一个扇形的周长是6cm,该扇形的中心角是1弧度,则该扇形的面积为( )cm2.
| A. | 2 | B. | 4 | C. | 6 | D. | 7 |
17.已知直线m,n与平面α,β,下列四个命题为真命题的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | ||
| C. | 若m∥α,n∥α,β∥α,则m∥n | D. | 若m∥n,m∥α,则n∥α |
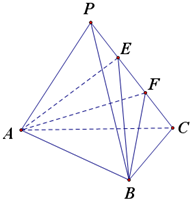 在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.
在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.