题目内容
3.已知y=f(x)为R上的连续可导的奇函数,当x>0时f′(x)+$\frac{f(x)}{x}$<0,则g(x)=f(x)+$\frac{2}{x}$的零点个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
分析 构造函数F(x)=xg(x)=xf(x)+2,则g(x)的零点即为F(x)的零点,根据导数和函数的奇偶性判断F(x)的单调性,根据F(x)的最值符号判断零点个数.
解答 解:由于函数g(x)=f(x)+$\frac{2}{x}$,可得x≠0,∴g(x)的零点与 xg(x)的零点相同,
令F(x)=xg(x)=xf(x)+2,
∴F′(x)=f(x)+xf′(x),
由于当x>0时,f′(x)+$\frac{f(x)}{x}$=$\frac{xf′(x)+f(x)}{x}<0$,
∴F′(x)=f(x)+xf′(x)<0,
∴F(x)在(0,+∞)上为减函数,
∵f(x)是奇函数,
∴F(x)=xg(x)=xf(x)+2为偶函数.
∵$\underset{lim}{x→0+}$F(x)=$\underset{lim}{x→0+}(xf(x)+2)$=2,
∴当$\underset{lim}{x→+∞}$F(x)≥0时,F(x)无零点,当$\underset{lim}{x→+∞}$F(x)<0时,F(x)有两个零点.
故选:D.
点评 本题考查了函数的零点与单调性,最值的关系,属于中档题.

练习册系列答案
相关题目
18.已知一个扇形的周长是6cm,该扇形的中心角是1弧度,则该扇形的面积为( )cm2.
| A. | 2 | B. | 4 | C. | 6 | D. | 7 |
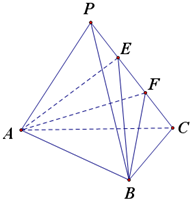 在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.
在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.