题目内容
已知某几何体的三视图如图所示,则该几何体的表面积为 .


考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是三棱锥,根据三视图可得三棱锥的一个侧面与底面垂直,结合直观图求相关几何量的数据,把数据代入棱锥的表面积公式计算.
解答:
解:由三视图知:几何体是三棱锥,且三棱锥的一个侧面与底面垂直,高为3,如图:
其中SO⊥平面ABC,SO=3,OD⊥AB,OE⊥BC,BO⊥AC,BO=1,OA=2,OC=1,
由三垂线定理得:SD⊥AB,SE⊥BC,
∴AB=
,BC=
,OE=
,OD=
,
∴SE=
=
,SD=
=
,
∴几何体的表面积S=
×3×3+
×3×1+
×
×
+
×
×
=
.
故答案为:
.

其中SO⊥平面ABC,SO=3,OD⊥AB,OE⊥BC,BO⊥AC,BO=1,OA=2,OC=1,
由三垂线定理得:SD⊥AB,SE⊥BC,
∴AB=
| 5 |
| 2 |
| ||
| 2 |
2
| ||
| 5 |
∴SE=
9+
|
| ||
| 2 |
9+
|
7
| ||
| 5 |
∴几何体的表面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 5 |
7
| ||
| 5 |
19+
| ||
| 2 |
故答案为:
19+
| ||
| 2 |

点评:本题考查了由三视图求几何体的表面积,根据三视图判断几何体的结构特征及求相关几何量的数据是解答本题的关键.

练习册系列答案
相关题目
执行如图所示的程序框图,若输出的x值为4,则输入的x值不可能为( )


| A、10 | B、8 | C、6 | D、5 |
某几何体的三视图如图所示,则该几何体的体积为( )


| A、54+54π |
| B、54+27π |
| C、27+27π |
| D、27+54π |
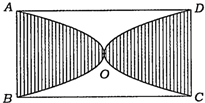 如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是
如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是