题目内容
3.已知函数f(x)=$\sqrt{3}$sinx+3cosx,当x∈[0,π]时,f(x)≥$\sqrt{3}$的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
分析 利用三角函数的辅助角公式求出当x∈[0,π]时,f(x)≥$\sqrt{3}$的等价条件,利用几何概型的概率公式即可得到结论.
解答 解:∵$\sqrt{3}$sinx+3cosx=2$\sqrt{3}$sin(x+$\frac{π}{3}$)≥$\sqrt{3}$,
∴sin(x+$\frac{π}{3}$)≥$\frac{1}{2}$,
∵x∈[0,π],x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],
∴$\frac{π}{3}$≤x+$\frac{π}{3}$≤$\frac{5π}{6}$,
∴0≤x≤$\frac{π}{2}$,
∴发生的概率为P=$\frac{1}{2}$,
故选:B.
点评 本题主要考查几何概型的概率的计算,利用辅助角公式求出不等式的等价条件是解决本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
13.已知p:x2-4x+3≤0,q:f(x)=$\frac{{x}^{2}+1}{x}$存在最大值和最小值,则p是q的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
14.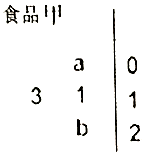 为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
 为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | 3 | D. | $\frac{7}{3}$ |
11.在[-1,2]内任取一个数a,则点(1,a)位于x轴下方的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
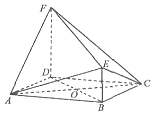 如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.
如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.