题目内容
15.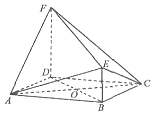 如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.
如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.(1)证明:平面ACF⊥平面BEFD.
(2)若$cos∠BAD=\frac{1}{5}$,求几何体ABCDEF的体积.
分析 (Ⅰ)证明AC⊥平面BEFD,利用面面垂直的判定定理证明平面ACF⊥平面BEFD;
(Ⅱ)求出AB长,利用体积公式求几何体的体积.
解答 (1)证明:∵四边形ABCD是菱形,∴AC⊥BD,
∵BE⊥平面ABCD,∴BE⊥AC,
∴AC⊥平面BEFD,
∴平面ACF⊥平面BEFD;
(2)解:设AC与BD的交点为O,AB=a(a>0),
由(1)得AC⊥平面BEFD,
∵BE⊥平面ABCD∴BE⊥BD,
∵DF∥BE,∴DF⊥BD,
∴BD2=EF2-(DF-BE)2=8,∴$BD=2\sqrt{2}$
∴${S_{四边形BEFD}}=\frac{1}{2}({BE+DF})•BD=3\sqrt{2}$,
∵$cos∠BAD=\frac{1}{5}$,∴$B{D^2}=A{B^2}+A{D^2}-2AB•AD•cos∠BAD=\frac{8}{5}{a^2}=8$
∴$a=\sqrt{5}$,
∴OA2=AB2-OB2=3,∴$OA=\sqrt{3}$
∴${V_{ABCDEF}}=2{V_{A-BEFD}}=\frac{2}{3}{S_{四边形BEFD}}•OA=2\sqrt{6}$.
点评 本题主要考查空间面面垂直的判定以及空间几何体的体积,要求熟练掌握相应的判定定理.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
6.已知抛物线y=ax2+2x-a-1(a∈R),恒过第三象限上一定点A,且点A在直线3mx+ny+1=0(m>0,n>0)上,则$\frac{1}{m}+\frac{1}{n}$的最小值为( )
| A. | 4 | B. | 12 | C. | 24 | D. | 36 |
3.已知函数f(x)=$\sqrt{3}$sinx+3cosx,当x∈[0,π]时,f(x)≥$\sqrt{3}$的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,$AC=BC=\frac{1}{2}A{A_1}=2$,点D是棱AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,$AC=BC=\frac{1}{2}A{A_1}=2$,点D是棱AA1的中点.