题目内容
12.计算:(1)0.064${\;}^{-\frac{1}{3}}$-(-$\frac{1}{8}$)0+16${\;}^{\frac{3}{4}}$+0.25${\;}^{\frac{1}{2}}$
(2)3${\;}^{lo{g}_{3}4}$-27${\;}^{\frac{2}{3}}$-lg0.01+lne3.
分析 (1)利用指数的运算法则即可得出.
(2)利用对数的运算法则即可得出.
解答 解:(1)原式=$0.{4}^{3×(-\frac{1}{3})}$-1+${2}^{4×\frac{3}{4}}$+$0.{5}^{2×\frac{1}{2}}$
=$\frac{5}{2}$-1+8+$\frac{1}{2}$=10.
(2)原式=4-${3}^{3×\frac{2}{3}}$-lg10-2+3=4-9+2+3=0.
点评 本题考查了指数与对数的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
3.已知函数f(x)=$\sqrt{3}$sinx+3cosx,当x∈[0,π]时,f(x)≥$\sqrt{3}$的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
1.已知点M在角θ终边的延长线上,且|OM|=2,则M的坐标为( )
| A. | (2cosθ,2sinθ) | B. | (-2cosθ,2sinθ) | C. | (-2cosθ,-2sinθ) | D. | (2cosθ,-2sinθ) |
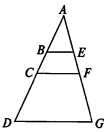
 在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.
在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.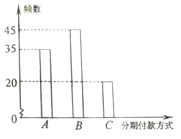 某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.