题目内容
18.已知各项均为正数的等比数列{an}满足:-a3,a2,a4成等差数列.(1)若a1=1,求{an}的前n项和Sn
(2)若bn=log2a2n+1,且数列{bn}的前n项和Tn=n2+3n,求a1.
分析 (1)只需要根据:-a3,a2,a4成等差数列建立方程求出公比,再代入等比数列的求和公式即可,
(2)先求出数列{bn}的通项公式,再利用等差数列的求和公式求出Tn,利用已知条件建立方程即可求出a1.
解答 解:(1)设{an}的公比为q,由条件可知q>0,
由-a3,a2,a4成等差数列,
∴2a2=-a3+a4,
∴2=q2-q,
解得q=2或q=-1(舍去),
又a1=1,
∴{an}的前n项和Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1;
(2)由(1)可知,an=a1•2n-1,
则bn=log2a2n+1=2n+log2a1,
∴Tn=$\frac{n(2+2n)}{2}$+nlog2a1=n2+3n
∴log2a1=2,
∴a1=4
点评 本题考查了等差数列等比数列的通项公式与求和公式的应用,意在考查学生的计算能力以及逻辑推理能力.

练习册系列答案
相关题目
9.某几何体的三视图如图,则该几何体的体积是( )
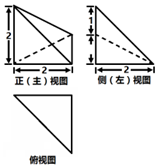

| A. | 4 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 2 |
6.已知抛物线y=ax2+2x-a-1(a∈R),恒过第三象限上一定点A,且点A在直线3mx+ny+1=0(m>0,n>0)上,则$\frac{1}{m}+\frac{1}{n}$的最小值为( )
| A. | 4 | B. | 12 | C. | 24 | D. | 36 |
13.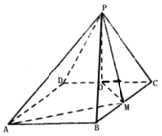 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{3}$ |
3.已知函数f(x)=$\sqrt{3}$sinx+3cosx,当x∈[0,π]时,f(x)≥$\sqrt{3}$的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |