题目内容
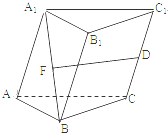 在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且
在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且| DF |
| AB |
| AC |
A、α=
| ||
B、α=-
| ||
C、α=1,β=-
| ||
D、α=-1,β=
|
考点:向量在几何中的应用
专题:空间向量及应用
分析:根据向量加法的多边形法则可得,
=
+
+
=
+
+
=
+
-
+
+
=
-
,从而可求α,β,
| DF |
| DC |
| CB |
| BF |
| 1 |
| 2 |
| C1C |
| CB |
| 1 |
| 2 |
| BA1 |
| 1 |
| 2 |
| A1A |
| AB |
| AC |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| AA1 |
| 1 |
| 2 |
| AB |
| AC |
解答:
解:根据向量加法的多边形法则以及已知可得,
=
+
+
=
+
+
=
+
-
+
+
=
-
,
∴α=
,β=-1,
故选A.
| DF |
| DC |
| CB |
| BF |
| 1 |
| 2 |
| C1C |
| CB |
| 1 |
| 2 |
| BA1 |
| 1 |
| 2 |
| A1A |
| AB |
| AC |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| AA1 |
| 1 |
| 2 |
| AB |
| AC |
∴α=
| 1 |
| 2 |
故选A.
点评:本题主要考查了平面向量加法的三角形法则及多边形法则的应用,解题的关键是要善于利用题目中正三棱柱的性质,把所求的向量用基本向量表示.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知f(x)=sinx则以下不等式正确的是( )
| A、f(3)<f(1)<f(2) |
| B、f(3)<f(2)<f(1) |
| C、f(1)<f(2)<f(3) |
| D、f(1)<f(3)<f(2) |
三棱锥的三个侧面都是直角三角形,且三个直角的顶点恰是三棱锥的顶点,则其底面一定是( )
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、等边三角形 |
△ABC中acosA=bcosB时,三角形的形状是( )
| A、正三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、前面说法都错 |
在独立性检验中,统计量x2有两个临界值:3.841和6.635;当x2>3.841时,有95%的把握说明两个事件有关,当x2>6.635时,有99%的把握说明两个事件相关,当x2≤3.841时,认为两个事件无关.在一项调查某种药是否对心脏病有治疗作用时,共调查了3000人,经计算的x2=4.56,根据这一数据分析,认为此药物与心脏病之间( )
| A、有95%的把握认为两者相关 |
| B、约有95%的心脏病患者使用药物有作用 |
| C、有99%的把握认为两者相关 |
| D、约有99%的心脏病患者使用药物有作用 |
已知两个相关变量x,y的回归方程是
=-2x+10,下列说法正确的是( )
 |
| y |
| A、当x的值增加1时,y的值一定减少2 |
| B、当x的值增加1时,y的值大约增加2 |
| C、当x=3时,y的准确值为4 |
| D、当x=3时,y的估计值为4 |
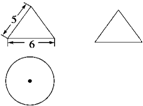 有一个几何体的三视图及其尺寸如图所示(单位:cm),则该几何体的表面积及体积为( )
有一个几何体的三视图及其尺寸如图所示(单位:cm),则该几何体的表面积及体积为( )| A、24π cm2,12π cm3 |
| B、15π cm2,12π cm3 |
| C、24π cm2,36π cm3 |
| D、以上都不正确 |