题目内容
正项数列{an}的前n项和为Sn,且Sn=(
)2.
(Ⅰ)证明数列{an}为等差数列并求其通项公式;
(Ⅱ)设cn=
,数列{cn}的前n项和为Tn,证明:
≤Tn<
.
| an+1 |
| 2 |
(Ⅰ)证明数列{an}为等差数列并求其通项公式;
(Ⅱ)设cn=
| 1 |
| anan+1 |
| 1 |
| 3 |
| 1 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件得(an-an-1-2)(an+an-1)=0,又数列{an}为正项数列,推导出{an}是首项为1公差为2的等差数列,由此求出an=1+(n-1)×2=2n-1.
(Ⅱ)由cn=
=
=
(
-
),由裂项求和法求出Tn=
.由此能证明
≤Tn<
.
(Ⅱ)由cn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:
(Ⅰ)证明:由Sn=(
)2,得a1=S1=(
)2,解得a1=1,
当n≥2时,an=Sn-Sn-1=(
)2-(
)2,
整理,得(an-an-1-2)(an+an-1)=0,
又数列{an}为正项数列,
∴an-an-1=2,n≥2.
∴{an}是首项为1公差为2的等差数列,
∴an=1+(n-1)×2=2n-1.
(Ⅱ)cn=
=
=
(
-
),
∴Tn=
(1-
+
-
+…+
-
)
=
(1-
)
=
.
∵n∈N*,∴Tn=
(1-
)<
,
Tn-Tn-1=
-
=
>0,
∴数列{Tn}是一个递增数列,∴Tn≥T1=
.
综上所述:
≤Tn<
.
| an+1 |
| 2 |
| a1+1 |
| 2 |
当n≥2时,an=Sn-Sn-1=(
| an+1 |
| 2 |
| an-1+1 |
| 2 |
整理,得(an-an-1-2)(an+an-1)=0,
又数列{an}为正项数列,
∴an-an-1=2,n≥2.
∴{an}是首项为1公差为2的等差数列,
∴an=1+(n-1)×2=2n-1.
(Ⅱ)cn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
=
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |
∵n∈N*,∴Tn=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
Tn-Tn-1=
| n |
| 2n+1 |
| n-1 |
| 2n-1 |
| 1 |
| (2n+1)(2n-1) |
∴数列{Tn}是一个递增数列,∴Tn≥T1=
| 1 |
| 3 |
综上所述:
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题考查等差数列的证明,考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
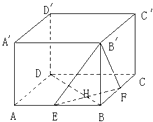 在棱长为a的正方体ABCD-A′B′C′D′中,如图E、F分别为棱AB与BC的中点,EF∩BD=H;
在棱长为a的正方体ABCD-A′B′C′D′中,如图E、F分别为棱AB与BC的中点,EF∩BD=H;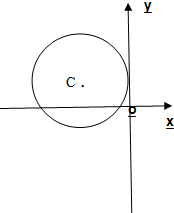 如图,已知位于y轴左侧的圆C与y轴相切于点(0,1),且被x轴分成的两段弧长之比为2:1,过点H(0,t)的直线l与圆C相交于M,N两点,且以MN为直径的圆恰好经过坐标原点O.
如图,已知位于y轴左侧的圆C与y轴相切于点(0,1),且被x轴分成的两段弧长之比为2:1,过点H(0,t)的直线l与圆C相交于M,N两点,且以MN为直径的圆恰好经过坐标原点O.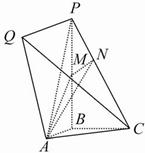 如图所示的几何体中,PB⊥平面ABC,PQ∥AB,PQ=PB=1,AB=BC=
如图所示的几何体中,PB⊥平面ABC,PQ∥AB,PQ=PB=1,AB=BC=