题目内容
1．若a，b∈R，i是虚数单位，且a+（b-2）i=1+i，则a-b的值为（ ）| A． | -2 | B． | -4 | C． | 2 | D． | 4 |
分析 利用复数相等即可得出．
解答 解：∵a+（b-2）i=1+i，∴a=1，b-2=1，
解得a=1，b=3．
则a-b=-2．
故选：A．
点评 本题考查了复数相等，考查推理能力与计算能力，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
11．某研究机构对高三学生的记忆力x和判断力y进行统计分析，得到下表数据
（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（2）试根据（2）中求出的线性回归方程，预测记忆力为9的同学的判断力．
（相关公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x，参考数据$\sum_{i=1}^{4}$xiyi=158，$\sum_{i=1}^{4}$x${\;}_{i}^{2}$=344）
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
（2）试根据（2）中求出的线性回归方程，预测记忆力为9的同学的判断力．
（相关公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$x，参考数据$\sum_{i=1}^{4}$xiyi=158，$\sum_{i=1}^{4}$x${\;}_{i}^{2}$=344）
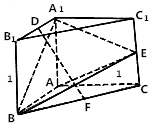已知三棱柱ABC-A1B1C1中，底面三角形ABC是直角三角形，四边形A1ACC1和四边形A1ABB1均为正方形，D，E，F分别是A1B1，C1C，BC的中点，AB=1．
9．在△ABC中，“A=$\frac{π}{4}$”是“sinA=$\frac{\sqrt{2}}{2}$”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充分必要条件 | D． | 既非充分也非必要条件 |
