题目内容
设定义在R上的函数f(x)=
,若关于x的方程[f(x)]2+bf(x)+c=0有7个不同的实根,则必有( )
|
| A、b<0且c=0 |
| B、b>0且c<0 |
| C、b<0且c>0 |
| D、b≥0且c=0 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:先画出f(x)的图象,观察图形可知若关于x的方程f2(x)+af(x)+b=3有三个不同实数解满足的条件,然后图象对称性求出三个根即可.
解答:
 解:作出f(x)的图象如图所示:
解:作出f(x)的图象如图所示:
设t=f(x),则方程[f(x)]2+bf(x)+c=0等价为t2+bt+c=0,
由图可知,只有当t=f(x)≥1时,方程t=f(x)有2个根.
当t=f(x)∈(0,1)时,t=f(x)有4个根.
当t=f(x)=0时,t=f(x)有3个根.
若关于x的方程f2(x)+af(x)+b=0有7个不同实数解,
则等价为t2+bt+c=0的两个根满足t1=0或t2∈(0,1),
则c=0,此时方程等价为t2+bt=0,
则t(t+b)=0,另外一个根t2=-b∈(0,1),
则-1<b<0.
即-1<b<0且c=0
故选:A
 解:作出f(x)的图象如图所示:
解:作出f(x)的图象如图所示:设t=f(x),则方程[f(x)]2+bf(x)+c=0等价为t2+bt+c=0,
由图可知,只有当t=f(x)≥1时,方程t=f(x)有2个根.
当t=f(x)∈(0,1)时,t=f(x)有4个根.
当t=f(x)=0时,t=f(x)有3个根.
若关于x的方程f2(x)+af(x)+b=0有7个不同实数解,
则等价为t2+bt+c=0的两个根满足t1=0或t2∈(0,1),
则c=0,此时方程等价为t2+bt=0,
则t(t+b)=0,另外一个根t2=-b∈(0,1),
则-1<b<0.
即-1<b<0且c=0
故选:A
点评:本题主要考查了函数与方程的综合运用,以及函数的图象与方程之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
设数列{an}的前n项和为Sn,令Tn=
,则称Tn为数列a1,a2…,an,的“理想数”,已知数列a1,a2,…a20的“理想数”为2100,则15,a1,a2,…an的“理想数”为( )
| S1+S2+…+Sn |
| n |
| A、2013 | B、2014 |
| C、2015 | D、2016 |
已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,AF=|
x0|,则x0=( )
| 5 |
| 4 |
| A、1 | B、2 | C、4 | D、8 |
一个几何体的三视图如图所示,则该几何体的底面积总和为( )
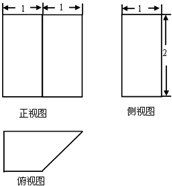

A、
| ||
| B、1 | ||
| C、3 | ||
| D、6 |
