题目内容
不等式|x-1|≤2的解集为: .(结果用集合或区间表示)
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:运用|x|≤a?-a≤x≤a,不等式|x-1|≤2即为-2≤x-1≤2,解出即可.
解答:
解:不等式|x-1|≤2即为-2≤x-1≤2,
即为-1≤x≤3,
则解集为[-1,3],
故答案为:[-1,3].
即为-1≤x≤3,
则解集为[-1,3],
故答案为:[-1,3].
点评:本题考查绝对值不等式的解法,考查运算能力,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
设定义在R上的函数f(x)=
,若关于x的方程[f(x)]2+bf(x)+c=0有7个不同的实根,则必有( )
|
| A、b<0且c=0 |
| B、b>0且c<0 |
| C、b<0且c>0 |
| D、b≥0且c=0 |
 若某几何体的三视图是如图所示的三个直角三角形,则该几何体的体积为( )
若某几何体的三视图是如图所示的三个直角三角形,则该几何体的体积为( )| A、60 | B、20 | C、30 | D、10 |
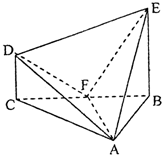 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=