题目内容
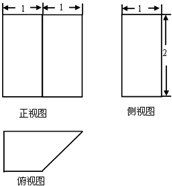
一个几何体的三视图如图所示，则该几何体的底面积总和为（ ）
A、
| ||
| B、1 | ||
| C、3 | ||
| D、6 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图，得出该几何体是底面为直角梯形，高为5的四棱柱，求出它的底面积总和即可．
解答：
解：根据几何体的三视图，得；
该几何体是底面为直角梯形，高为2的四棱柱，
∴该几何体的底面积是两个上底为1，下底为2，高为1的梯形，
∴底面积总和是
S=2×（1+2）×1×
=3．
故选：C．
该几何体是底面为直角梯形，高为2的四棱柱，
∴该几何体的底面积是两个上底为1，下底为2，高为1的梯形，
∴底面积总和是
S=2×（1+2）×1×
| 1 |
| 2 |
故选：C．
点评：本题考查了空间几何体的三视图的应用问题，解题时应根据几何体的三视图，得出该几何体是什么图形，是基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
某公司准备进行两种组合投资，稳健型组合投资是由每份金融投资20万元，房地产投资30万元组成；进取型组合投资是由每份金融投资40万元，房地产投资30万元组成．已知每份稳健型组合投资每年可获利10万元，每份进取型组合投资每年可获利15万元．若可作投资用的资金中，金融投资不超过160万元，房地产投资不超过180万元，要使一年获利总额最多，则稳健型组合投资与进取型组合，合投资分别注入的份数分别为（ ）
| A、x=4，y=2 |
| B、x=3，y=3 |
| C、x=5，y=1 |
| D、x=5，y=2 |
设定义在R上的函数f（x）=
，若关于x的方程[f（x）]2+bf（x）+c=0有7个不同的实根，则必有（ ）
|
| A、b＜0且c=0 |
| B、b＞0且c＜0 |
| C、b＜0且c＞0 |
| D、b≥0且c=0 |