题目内容

函数y=-2sin（
1
2
x-
π
3
）的最小正周期是（　　）
A、4πB、3πC、2πD、π
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：由条件根据y=Asin（ωx+φ）的周期等于 T=
2π
ω
，可得结论．
解答： 解：函数y=-2sin（
1
2
x-
π
3
）的最小正周期T=
2π
1
2
=4π，
故选：A．
点评：本题主要考查三角函数的周期性及其求法，利用了y=Asin（ωx+φ）的周期等于 T=
2π
ω
，属于基础题．
练习册系列答案
相关题目
若一个点是一个指数函数图象与对数函数的图象的公共点，则称此点是“好点”，有M（1，1），N（1，2），P（2，1），Q（2，2），G（2，0）中“好点”的个数是
 
．
函数y=
x
x2+a
的大致图象如图所示，则（　　）
A、a∈（-1，0）
B、a∈（0，1）
C、a∈（-∞，1）
D、a∈（1，+∞）
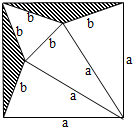如图，把边长为a的正方形剪去图中的阴影部分，沿图中所画的折成一个正三棱锥，则这个正三棱锥的高是（　　）
A、
1
3
3+2
3
a
B、
1
3
3-
3
a
C、
1
3
2+
3
a
D、
1
3
3+3
3
a
和两条异面直线都平行的直线（　　）
A、只有一条B、两条
C、无数条D、不存在
下列命题正确的是（　　）
A、有一条侧棱与底面两边垂直的棱柱是直棱柱
B、有一个侧面是矩形的棱柱是直棱柱
C、有两个侧面是矩形的棱柱是直棱柱
D、有两个相邻侧面是矩形的棱柱是直棱柱
下列关系式中正确的是（　　）
A、sin10°＜cos10°＜sin160°
B、sin160°＜sin10°＜cos10°
C、sin10°＜sin160°＜cos10°
D、sin160°＜cos10°＜sin10°
给出以下四个命题：p：若x2-3x+2=0，则x=1或x=2；q：若2≤x＜3，则（x-2）（x-3）≤0；r：若x=y=0，则x2+y2=0；s：若x2y2，则xy或x-y（　　）
A、p的逆命题为真
B、q的否命题为真
C、r的否命题为假
D、s的逆命题为真
已知函数f（x）=（x-a）2+（
2
x
-a）2-a2+2（x＞0，a∈R），若函数f（x）有四个不同的零点，则a的取值范围是（　　）
A、-3
2
＜a＜3
2
B、a＞3
2
C、2
2
＜a＜3
2
D、a＞2
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网