题目内容
10.如图1,菱形ABCD的边长为12,∠BAD=60°,AC交BD于点O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M,N分别是棱BC,AD的中点,且DM=6$\sqrt{2}$.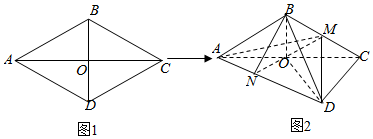
(Ⅰ)求证:OD⊥平面ABC;
(Ⅱ)求三棱锥M-ABN的体积.
分析 (Ⅰ)由ABCD是菱形,可得AD=DC,OD⊥AC,求解三角形可得OD=6,结合M是BC的中点,求出OM、MD,可得OD2+OM2=MD2,得DO⊥OM,由线面垂直的判定可得OD⊥面ABC;
(Ⅱ)取线段AO的中点E,连接NE.可得NE∥DO.由(Ⅰ)得OD⊥面ABC,可得NE⊥面ABC,求出△ABM的面积,然后利用等积法求得三棱锥M-ABN的体积.
解答 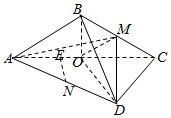 (Ⅰ)证明:∵ABCD是菱形,∴AD=DC,OD⊥AC,
(Ⅰ)证明:∵ABCD是菱形,∴AD=DC,OD⊥AC,
在△ADC中,AD=DC=12,∠ADC=120°,∴OD=6,
又M是BC的中点,∴$OM=\frac{1}{2}AB=6,MD=6\sqrt{2}$,
∵OD2+OM2=MD2,则DO⊥OM,
∵OM,AC?面ABC,OM∩AC=O,
∴OD⊥面ABC;
(Ⅱ)解:取线段AO的中点E,连接NE.
∵N是棱AD的中点,∴NE=$\frac{1}{2}DO$且NE∥DO.
由(Ⅰ)得OD⊥面ABC,∴NE⊥面ABC,
在△ABM中,AB=12,BM=6,∠ABM=120°,
∴${S}_{△ABM}=\frac{1}{2}•AB•BM•sin∠ABM$=$\frac{1}{2}×12×6×\frac{\sqrt{3}}{2}=18\sqrt{3}$.
∴${V_{M-ABN}}=\frac{1}{2}{V_{M-ABD}}=\frac{1}{2}{V_{D-ABM}}=\frac{1}{2}•\frac{1}{3}{S_{△ABM}}•OD=18\sqrt{3}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
20.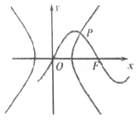 如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )
如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )
 如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )
如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )| A. | x±y=0 | B. | x±2y=0 | C. | x±$\sqrt{3}$y=0 | D. | 2x±y=0 |
5.函数f(x)=lnx-$\frac{2}{x-1}$的零点所在的大致区间是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
15.“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据(xi,yi)(i=1,2,…,6),如表所示:
已知$\overline{y}$=$\frac{1}{6}$$\sum_{i=1}^{6}{y}_{i}$=80
(Ⅰ)求出q的值;
(Ⅱ)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\overrightarrow{a}$
(Ⅲ)用$\stackrel{∧}{{y}_{i}}$表示用正确的线性回归方程得到的与xi对应的产品销量的估计值.当销售数据(xi,yi)的残差的绝对值|$\stackrel{∧}{{y}_{i}}$-yi|≤1时,则将销售数据(xi,yi)称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有一个是“好数据”的概率.
| 试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
(Ⅰ)求出q的值;
(Ⅱ)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\overrightarrow{a}$
(Ⅲ)用$\stackrel{∧}{{y}_{i}}$表示用正确的线性回归方程得到的与xi对应的产品销量的估计值.当销售数据(xi,yi)的残差的绝对值|$\stackrel{∧}{{y}_{i}}$-yi|≤1时,则将销售数据(xi,yi)称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有一个是“好数据”的概率.
19.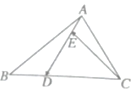 如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )
如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )
 如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )
如图,在△ABC中,点D在BC边上,且CD=2DB,点E在AD边上,且AD=3AE,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{CE}$为( )| A. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{8}{9}\overrightarrow{AC}$ | B. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{8}{9}\overrightarrow{AC}$ | C. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{7}{9}\overrightarrow{AC}$ | D. | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{7}{9}\overrightarrow{AC}$ |