题目内容
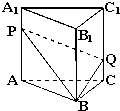 如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )
如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )| A、2:1 | B、3:1 |
| C、3:2 | D、4:3 |
考点:棱柱、棱锥、棱台的体积
专题:分割补形法,空间位置关系与距离
分析:把直三棱柱ABC-A1B1C1分割为:B-APQC,B-C1QPA1,B-B1A1C1,运用体积公式求解,得出结论.
解答:
 解:设直三棱柱ABC-A1B1C1的体积为V,
解:设直三棱柱ABC-A1B1C1的体积为V,
∵连接BA1,BC1,点P、Q分别在棱AA1和CC1上,AP=C1Q,
∴四棱锥的B-APQC,B-C1QPA1,的底面积相等
∴把直三棱柱ABC-A1B1C1分割为:B-APQC,B-C1QPA1,B-B1A1C1,
∴三棱锥的B-B1A1C1为
V,
∴四棱锥B-APQC,B-C1QPA1的体积之和为:V-
V=
,
∵四棱锥的B-APQC,B-C1QPA1,的底面积,高相等.
∴四棱锥的B-APQC,B-C1QPA1,的体积相等,
即为
V,
∴棱锥B-APQC,B-C1QPA1,B-B1A1C1的体积相等,为
V,
∴平面BPQ把三棱柱分成两部分的体积比为2:1,
故选:A
 解:设直三棱柱ABC-A1B1C1的体积为V,
解:设直三棱柱ABC-A1B1C1的体积为V,∵连接BA1,BC1,点P、Q分别在棱AA1和CC1上,AP=C1Q,
∴四棱锥的B-APQC,B-C1QPA1,的底面积相等
∴把直三棱柱ABC-A1B1C1分割为:B-APQC,B-C1QPA1,B-B1A1C1,
∴三棱锥的B-B1A1C1为
| 1 |
| 3 |
∴四棱锥B-APQC,B-C1QPA1的体积之和为:V-
| 1 |
| 3 |
| 2V |
| 3 |
∵四棱锥的B-APQC,B-C1QPA1,的底面积,高相等.
∴四棱锥的B-APQC,B-C1QPA1,的体积相等,
即为
| 1 |
| 3 |
∴棱锥B-APQC,B-C1QPA1,B-B1A1C1的体积相等,为
| 1 |
| 3 |
∴平面BPQ把三棱柱分成两部分的体积比为2:1,
故选:A
点评:本题综合考查了空间几何体的体积求解方法,分割思想,等底等高求解,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
出租车按如下方法收费:起步价7元,可行3km(不含3km);3km到7km(不含7km)按1.6元/km计价(不足1km按1km计算);7km以后按2.2元/km计价,到目的地结算时还需付1元的燃油附加费.若从甲地坐出租车到乙地(路程12.2km),需付车费(精确到1元)( )
| A、28元 | B、27元 |
| C、26元 | D、25元 |
有一抛物线型拱桥,当水面离拱顶2米时,水面宽4米,则当水面下降1米后,水面宽度为( )
| A、9 | ||
| B、4.5 | ||
C、
| ||
D、2
|
已知点P,A,B在双曲线
-
=1上,直线AB过坐标原点,且直线PA、PB的斜率之积为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
已知函数f(x)=loga[(a+1)x2-x-7]在[2,3]上是增函数,则实数a的取值范围是( )
A、(
| ||||
B、(
| ||||
| C、(2,+∞) | ||||
D、(
|