题目内容
给出以下四个命题,所有真命题的序号为 .
①从总体中抽取样本(x1,y1),(x2,y2),…,(xn,yn),若记
=
xi,
=
yi,则回归直线y=bx+a必过点(
,
);
②将函数y=cos 2x的图象向右平移
个单位,得到函数y=sin(2x-
)的图象;
③已知数列{an},那么“对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上”是“{an}为等差数列”的充分不必要条件;
④命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|≥2,则-2<x<2”.
①从总体中抽取样本(x1,y1),(x2,y2),…,(xn,yn),若记
. |
| x |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| y |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| x |
. |
| y |
②将函数y=cos 2x的图象向右平移
| π |
| 3 |
| π |
| 6 |
③已知数列{an},那么“对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上”是“{an}为等差数列”的充分不必要条件;
④命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|≥2,则-2<x<2”.
考点:命题的真假判断与应用
专题:简易逻辑
分析:本题①根据回归直线的特征判断命题是否正确;②根据函数图象平移前后解析式的联系,判断命题是否正确;③等差数列的通项特征,得到对应 的点的位置关系,从而判断命题是否正确;④命题否定的规律,得到原命题的否命题,从而判断命题是否正确.
解答:
解:①从总体中抽取样本(x1,y1),(x2,y2),…,(xn,yn),
若记
=
xi,
=
yi,则回归直线y=bx+a必过点(
,
).
根据参数b的算法可知,命题①正确;
②将函数y=cos 2x的图象向右平移
个单位,
得到函数y=cos 2(x-
)=cos(2x-
),
故命题②是假命题;
③若{an}为等差数列,
记首项为a1,公差为d,an=a1+(n-1)d=dn+(a1-d),
∴点Pn(n,an)在直线y=dx+(a1-d)上.
若d≠2时,点Pn(n,an)就一定不在直线y=2x+1上;
若对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上,
则有an=2n+1,an+1-an=2,“{an}为等差数列;
∴命题③正确;
④命题“若|x|≥2,则x≥2或x≤-2”的否命题是:
“若x<2,则-2<x<2”,
故命题④是错误的.
综上,正确的命题有:①③.
故答案为:①③.
若记
. |
| x |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| y |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| x |
. |
| y |
根据参数b的算法可知,命题①正确;
②将函数y=cos 2x的图象向右平移
| π |
| 3 |
得到函数y=cos 2(x-
| π |
| 3 |
| 2π |
| 3 |
故命题②是假命题;
③若{an}为等差数列,
记首项为a1,公差为d,an=a1+(n-1)d=dn+(a1-d),
∴点Pn(n,an)在直线y=dx+(a1-d)上.
若d≠2时,点Pn(n,an)就一定不在直线y=2x+1上;
若对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上,
则有an=2n+1,an+1-an=2,“{an}为等差数列;
∴命题③正确;
④命题“若|x|≥2,则x≥2或x≤-2”的否命题是:
“若x<2,则-2<x<2”,
故命题④是错误的.
综上,正确的命题有:①③.
故答案为:①③.
点评:本题考查了命题真假的判断,还考查了抽样统计、三角函数图象变换、数列通项、充要条件、命题的否定等知识,本题难度不大,属于基础题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列说法中:
①所有幂函数的图象都经过点(1,1)和(0,0);
②所有幂函数的图象都不经过第四象限;
③函数y=x0的图象是一条直线;
④幂函数可能是奇函数,也可能是偶函数,也可能既不是奇函数也不是偶函数;
正确说法的个数是( )
①所有幂函数的图象都经过点(1,1)和(0,0);
②所有幂函数的图象都不经过第四象限;
③函数y=x0的图象是一条直线;
④幂函数可能是奇函数,也可能是偶函数,也可能既不是奇函数也不是偶函数;
正确说法的个数是( )
| A、0 | B、1 | C、2 | D、3 |
有一抛物线型拱桥,当水面离拱顶2米时,水面宽4米,则当水面下降1米后,水面宽度为( )
| A、9 | ||
| B、4.5 | ||
C、
| ||
D、2
|
已知
,
,
是空间的一个基底,设
=
+
,
=
-
,则下列向量中可以与
,
一起构成空间的另一个基底的是( )
| a |
| b |
| c |
| p |
| a |
| b |
| q |
| a |
| b |
| p |
| q |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
已知函数①y=3x;②y=lnx;③y=x-1;④y=x
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的对应顺序一致的是( )
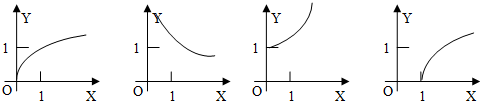
| 1 |
| 2 |
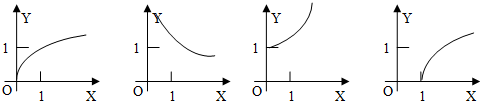
| A、④③①② | B、②③①④ |
| C、④①③② | D、②①③④ |