题目内容
函数f（x）=
+2
的定义域为 ．
| 1 |
| x-1 |
| x+1 |
考点：函数的定义域及其求法
专题：计算题,函数的性质及应用
分析：要使函数有意义，则需x+1≥0且x-1≠0，解得即可，注意用区间或集合表示．
解答：
解：要使函数有意义，则需
x+1≥0且x-1≠0，
解得，x≥-1且x≠1，
则定义域为[-1，1）∪（1，+∞）．
故答案为：[-1，1）∪（1，+∞）．
x+1≥0且x-1≠0，
解得，x≥-1且x≠1，
则定义域为[-1，1）∪（1，+∞）．
故答案为：[-1，1）∪（1，+∞）．
点评：本题考查函数的定义域的求法：注意偶次根式被开方式非负，分式分母不为0，考查运算能力，属于基础题．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
设全集R，A={x|x＞0}，B={x|x＞1}，则A∩∁RB=（ ）
| A、{x|0≤x＜1} |
| B、{x|0＜x≤1} |
| C、{x|x＜0} |
| D、{x|x＞1} |
下列两集合表示同一集合的是（ ）
| A、M={1，2}，N={（1，2）} |
| B、M={y=lgx2}，N={y=2lgx} |
| C、M={x|x+y=1}，N={y|x+y=1} |
| D、M={y|y=x2}，N={y|y=2x} |
集合{（x，y）|xy≥0，x∈R，y∈R}是指（ ）
| A、第一象限内的所有点 |
| B、第三象限内的所有点 |
| C、第一象限和第三象限内的所有点 |
| D、不在第二象限、第四象限内的所有点 |
出租车按如下方法收费：起步价7元，可行3km（不含3km）；3km到7km（不含7km）按1.6元/km计价（不足1km按1km计算）；7km以后按2.2元/km计价，到目的地结算时还需付1元的燃油附加费．若从甲地坐出租车到乙地（路程12.2km），需付车费（精确到1元）（ ）
| A、28元 | B、27元 |
| C、26元 | D、25元 |
某几何体的三视图如图所示，根据图中标出的数据，可得这个几何体的体积为（ ）
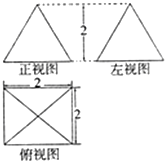
A、4+4
| ||
B、4+4
| ||
C、
| ||
| D、12 |
有一抛物线型拱桥，当水面离拱顶2米时，水面宽4米，则当水面下降1米后，水面宽度为（ ）
| A、9 | ||
| B、4.5 | ||
C、
| ||
D、2
|