题目内容
4.当实数x,y满足x2+y2=1时,|x+2y+a|+|3-x-2y|的取值与x,y均无关,则实数a的取范围是[$\sqrt{5}$,+∞).分析 根据实数x,y满足x2+y2=1,设x=cosθ,y=sinθ,求出x+2y的取值范围,再讨论a的取值范围,求出|x+2y+a|+|3-x-2y|的值与x,y均无关时a的取范围.
解答 解:∵实数x,y满足x2+y2=1,
可设x=cosθ,y=sinθ,
则x+2y=cosθ+2sinθ=$\sqrt{5}$sin(θ+α),其中α=arctan2;
∴-$\sqrt{5}$≤x+2y≤$\sqrt{5}$,
∴当a≥$\sqrt{5}$时,
|x+2y+a|+|3-x-2y|=(x+2y+a)+(3-x-2y)=a+3,其值与x,y均无关;
∴实数a的取范围是[$\sqrt{5}$,+∞).
故答案为:$[{\sqrt{5}}\right.,+∞)$.
点评 本题考查了圆的方程以及绝对值的定义与应用问题,也考查了转化思想的应用问题,是综合性题目.

练习册系列答案
相关题目
14.圆x2+y2-2x-2y-2=0和圆x2+y2+6x-2y+6=0的公切线条数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.某中学的高一、高二、高三共有学生1350人,其中高一500人,高三比高二少50人,为了解该校学生健康状况,现采用分层抽样方法进行调查,在抽取的样本中有高一学生120人,则该样本中的高二学生人数为( )
| A. | 80 | B. | 96 | C. | 108 | D. | 110 |
12.设a,b∈R,则“$\left\{\begin{array}{l}{a+b>2}\\{ab>1}\end{array}\right.$”是“a>1且b>1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分又非必要条件 |
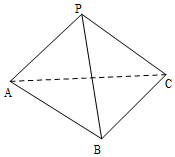 在正三棱锥P-ABC中,已知底面等边三角形的边长为6,侧棱长为4.
在正三棱锥P-ABC中,已知底面等边三角形的边长为6,侧棱长为4.