题目内容
18．设函数f（2x）的定义域为（1，2），求f（$\sqrt{{x}^{2}-1}$）的定义域（-$\sqrt{17}$，-$\sqrt{5}$）∪（$\sqrt{5}$，$\sqrt{17}$）．分析 根据函数f（2x）的定义域求出f（x）的定义域，
再由此求出f（$\sqrt{{x}^{2}-1}$）的定义域．
解答 解：函数f（2x）的定义域为（1，2），
∴x∈（1，2），∴2x∈（2，4），
∴f（x）的定义域是（2，4）；
令2＜$\sqrt{{x}^{2}-1}$＜4，
得4＜x2-1＜16，
即5＜x2＜17，
解得-$\sqrt{17}$＜x＜-$\sqrt{5}$或$\sqrt{5}$＜x＜$\sqrt{17}$，
∴f（$\sqrt{{x}^{2}-1}$）的定义域为（-$\sqrt{17}$，-$\sqrt{5}$）∪（$\sqrt{5}$，$\sqrt{17}$）．
故答案为：$（{-\sqrt{17}，-\sqrt{5}}）∪（{\sqrt{5}，\sqrt{17}}）$．
点评 本题考查了函数的定义域及其求法，是基础题．
①给出f（x）的定义域为[a，b]，f[g（x）]的定义域，就是不等式a≤g（x）≤b得x得取值集合，
②给出f[g（x）]的定义域为[a，b]，求解f（x）的定义域，就是在x∈[a，b]内的g（x）的值域．
练习册系列答案
相关题目
8．
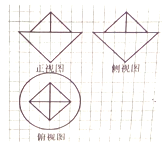如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）| A． | 9（$\sqrt{2}$+1）π+8$\sqrt{3}$ | B． | 9（$\sqrt{3}$+2）π+4$\sqrt{3}$-8 | C． | 9（$\sqrt{3}$+2）π+4$\sqrt{3}$ | D． | 9（$\sqrt{2}$+1）π+8$\sqrt{3}$-8 |
9．命题“若a≥-1，则x+a≥1nx”的否定是（ ）
| A． | 若a＜-1，则x+a＜1nx | B． | 若a≥-1，则x+a＜1nx | ||
| C． | 若a＜-1，则x+a≥1nx | D． | 若a≥-1，则x+a≤1nx |
6．函数f（x）在定义域R内可导，f（x）=f（2-x），当x∈（1，+∞）时，（x-1）f′（x）＜0，设a=f（log32），b=f（log52），c=f（log25），则（ ）
| A． | c＜a＜b | B． | c＜b＜a | C． | a＜b＜c | D． | b＜a＜c |
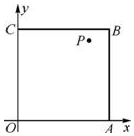如图，在边长为1的正方形OABC内任取一点P（x，y）．