题目内容
13.方程sin2x=cosx,x∈[0,2π]的解集是{$\frac{π}{2}$,$\frac{3π}{2}$,$\frac{π}{6}$,$\frac{5π}{6}$}.分析 方程即cosx=0或sinx=$\frac{1}{2}$,结合正弦函数、余弦函数的图象以及x∈[0,2π],分别求得x的值,可得结论.
解答 解:方程sin2x=cosx,即2sinxcosx=cosx,即 cosx=0或sinx=$\frac{1}{2}$.
由cosx=0,x∈[0,2π],可得x=$\frac{π}{2}$或$\frac{3π}{2}$;由sinx=$\frac{1}{2}$,x∈[0,2π],可得x=$\frac{π}{6}$或x=$\frac{5π}{6}$,
综上可得,方程sin2x=cosx,x∈[0,2π]的解集是{$\frac{π}{2}$,$\frac{3π}{2}$,$\frac{π}{6}$,$\frac{5π}{6}$},
故答案为:{$\frac{π}{2}$,$\frac{3π}{2}$,$\frac{π}{6}$,$\frac{5π}{6}$}.
点评 本题主要考查三角方程的解法,正弦函数、余弦函数的图象,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
4.{an}是首项为1,公差为3的等差数列,如果an=2 014,则序号n等于( )
| A. | 667 | B. | 668 | C. | 669 | D. | 672 |
5.设a,b是两条不同的直线,α,β为两个不重合的平面,下列命题中的真命题的是( )
| A. | 若a,b与α所成的角相等,则a∥b | B. | 若a∥α,b∥β,α∥β,则a∥b | ||
| C. | 若a?α,b?β,α⊥β,则 a⊥b | D. | 若a⊥α,b⊥β,α∥β,则a∥b |
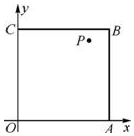 如图,在边长为1的正方形OABC内任取一点P(x,y).
如图,在边长为1的正方形OABC内任取一点P(x,y).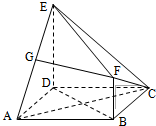 在多面体ABCDEF中,四边形ABCD为正方形,AD=DE=2BF=2,ED⊥平面ABCD,FB∥ED.
在多面体ABCDEF中,四边形ABCD为正方形,AD=DE=2BF=2,ED⊥平面ABCD,FB∥ED.