题目内容
5.若曲线y=sinx(0<x<π)在点(x0,sinx0)处的切线与直线y=$\frac{1}{2}$x+5平行,则x0的值为$\frac{π}{3}$.分析 利用直线平行:斜率相等,求出切线的斜率,再利用导数在切点处的值是曲线的切线斜率,求出切线斜率,列出方程即得.
解答 解:∵y=sinx,
∴y′=cosx,
∵曲线y=sinx(0<x<π)在点(x0,sinx0)处的切线
与直线y=$\frac{1}{2}$x+5平行,
∴cosx0=$\frac{1}{2}$,
∵0<x0<π
∴x0=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 此题主要考查导数的计算,以及利用导数研究曲线上某点切线方程,属于基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
15.已知数列{an}的前n项和S${\;}_{n}=A{q}^{n}+B(q≠0)$,则“A=-B“是“数列{an}是等比数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1(a>0)的离心率为2,则a等于( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
15.函数f(x)=x-2cosx在区间$[-\frac{π}{2},0]$上的最小值是( )
| A. | $-\frac{π}{2}$ | B. | -2 | C. | $-\frac{π}{3}-1$ | D. | $-\frac{π}{6}-\sqrt{3}$ |
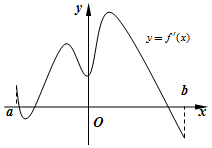 函数f(x)的定义域为开区间(a,b),其导函数f'(x)在(a,b)图象如图所示,则函数f(x)在开区间(a,b)内的极小值的个数是1个.
函数f(x)的定义域为开区间(a,b),其导函数f'(x)在(a,b)图象如图所示,则函数f(x)在开区间(a,b)内的极小值的个数是1个.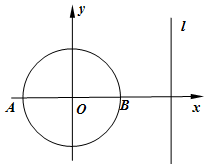 如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.
如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.