题目内容
已知在R上处处可导的函数f（x）满足，（x-2）f′（x）＜0，且f（1）=f（5），则不等式f（2x-1）＞f（1）的解集是（ ）
| A、（-∞，1） |
| B、（1，3） |
| C、（1，2）∪（2，3） |
| D、（3，+∞） |
考点：导数的运算
专题：导数的概念及应用
分析：需要分类讨论，当x＞2时或x＜2时，利用函数的单调性得到不等式，解得即可．
解答：
解：∵（x-2）f′（x）＜0，
当x＞2时，f′（x）＜0，故函数f（x）为减函数，
∵f（1）=f（5），不等式f（2x-1）＞f（1）=f（5），
∴2x-1＜5，
解得2＜x＜3，
当x＜2时，f′（x）＞0，故函数f（x）为增函数，
∵f（1）=f（5），不等式f（2x-1）＞f（1），
∴2x-1＞1，
解得1＜x＜2，
综上所述：不等式f（2x-1）＞f（1）的解集是（1，2）∪（2，3）
当x＞2时，f′（x）＜0，故函数f（x）为减函数，
∵f（1）=f（5），不等式f（2x-1）＞f（1）=f（5），
∴2x-1＜5，
解得2＜x＜3，
当x＜2时，f′（x）＞0，故函数f（x）为增函数，
∵f（1）=f（5），不等式f（2x-1）＞f（1），
∴2x-1＞1，
解得1＜x＜2，
综上所述：不等式f（2x-1）＞f（1）的解集是（1，2）∪（2，3）
点评：本题主要考查了导数的应用，以及不等式的解法，属于基础题．
练习册系列答案
相关题目
若a＜0、b＞0，则下列不等式中正确的是（ ）
| A、|a|＞|b| | ||||
| B、a2＜b2 | ||||
C、
| ||||
D、
|
下列说法中正确的有（ ）
①若任取x1，x2∈I，当x1＜x2时，f （x1）＜f （x2），则y=f （x）在I上是增函数；
②函数y=x2在R上是增函数；
③函数y=-
在定义域上是增函数；
④y=
的单调递减区间是（-∞，0）∪（0，+∞）．
①若任取x1，x2∈I，当x1＜x2时，f （x1）＜f （x2），则y=f （x）在I上是增函数；
②函数y=x2在R上是增函数；
③函数y=-
| 1 |
| x |
④y=
| 1 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
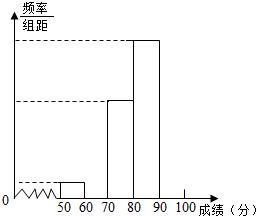中日“钓鱼岛争端”问题越来越引起社会关注，我校对高一600名学生进行了一次“钓鱼岛”知识测试，并从中抽取了部分学生的成绩（满分100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图．已知函数f（x）=
是偶函数，则g（-8）的值等于（ ）
|
| A、-8 | B、-3 | C、3 | D、8 |