题目内容
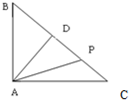 如图,已知△ABC中,AB=3,AC=4,BC=5,AD⊥BC于D点,点P为BC边所在直线上的一个动点,则
如图,已知△ABC中,AB=3,AC=4,BC=5,AD⊥BC于D点,点P为BC边所在直线上的一个动点,则| AP |
| AD |
| A、最大值为9 | ||
B、为定值
| ||
| C、最小值为3 | ||
| D、与P的位置有关 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由AB=3,AC=4,BC=5,32+42=52,利用勾股定理的逆定理可得∠BAC=90°.利用
AB•AC=
AD•BC,可得AD=
.再利用数量积的定义和投影的定义即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
| AB•AC |
| BC |
解答:
解:∵AB=3,AC=4,BC=5,32+42=52,∴∠BAC=90°.
∵AD⊥BC于D点,
∴
AB•AC=
AD•BC,
∴AD=
=
=
.
∴
•
=|
| |
|cos<
,
>=|
|2=(
)2=
.
故选:B.
∵AD⊥BC于D点,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AB•AC |
| BC |
| 3×4 |
| 5 |
| 12 |
| 5 |
∴
| AP |
| AD |
| AP |
| AD |
| AP |
| AD |
| AD |
| 12 |
| 5 |
| 144 |
| 25 |
故选:B.
点评:本题考查了勾股定理的逆定理、数量积的定义和投影的定义,属于基础题.

练习册系列答案
相关题目
若P=
+
,Q=
+
(a≥0),则P,Q的大小关系为( )
| a+2 |
| a+5 |
| a+3 |
| a+4 |
| A、P>Q | B、P=Q |
| C、P<Q | D、由a的取值确定 |
228与1995的最大公约数为( )
| A、57 | B、39 | C、46 | D、58 |
抛物线y2=8x的焦点到双曲线x2-
=1的渐近线的距离是( )
| y2 |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
设直线y=t与函数f(x)=x
,g(x)=ex的图象分别交于点M,N,则当|MN|达到最小时t的值为( )
| 1 |
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
程序框图如图所示,则该程序运行后输出k的值是( )


| A、3 | B、4 | C、5 | D、6 |
用反证法证明:某方程“方程有唯一解”中,假设正确的是该方程( )
| A、无解 | B、有两个解 |
| C、至少两解 | D、至少有两个解或无解 |
已知关于x的不等式(a2-3)x2+5x-2>0的解集是{x|
<x<2},则实数a的值是( )
| 1 |
| 2 |
| A、1 | B、-1 | C、±1 | D、0 |
函数y=x2•cosx的导数为( )
| A、2xcosx+x2sinx |
| B、x2sinx-2xcosx |
| C、2xcosx-x2sinx |
| D、x2cosx-2xsinx |